题目内容
“b≥-1”是“函数y=x2+bx+1(x∈[1,+∞))为增函数”的( )
| A、充分但不必要条件 | B、必要但不充分条件 | C、充要条件 | D、既不是充分条件也不是必要条件 |
分析:利用对称轴公式求出二次函数的对称轴,根据二次函数的单调区间与对称轴的关系求出“函数y=x2+bx+1(x∈[1,+∞))为增函数的充要条件,判断由前者成立是否能推出后者成立,反之后者成立能否推出前者成立,利用充要条件定义得到结论.
解答:解:∵函数y=x2+bx+1的对称轴为x=-
若函数y=x2+bx+1(x∈[1,+∞))为增函数
等价于-
≤1
解得b≥-2
∵b≥-1成立时,b≥-2一定成立
反之,当b≥-2成立时,b≥-1不一定成立
∴“b≥-1”是“函数y=x2+bx+1(x∈[1,+∞))为增函数”的充分但不必要条件
故选A
| b |
| 2 |
若函数y=x2+bx+1(x∈[1,+∞))为增函数
等价于-
| b |
| 2 |
解得b≥-2
∵b≥-1成立时,b≥-2一定成立
反之,当b≥-2成立时,b≥-1不一定成立
∴“b≥-1”是“函数y=x2+bx+1(x∈[1,+∞))为增函数”的充分但不必要条件
故选A
点评:解决二次函数的单调性问题、值域问题一般利用二次函数的对称轴与区间的关系;判断一个命题是另一个命题的什么条件,应该先化简各个命题再进行判断.

练习册系列答案
相关题目
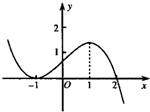 已知函数f(x)的导函数f′(x)的图象如图所示,那么
已知函数f(x)的导函数f′(x)的图象如图所示,那么