题目内容
函数f(x)的定义域为R，并满足以下条件：
①对任意x∈R，有f(x)＞0；
②对任意x，y∈R，有f(xy)=[f(x)]y；
③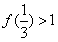
；
(Ⅰ)求f(0)的值；
(Ⅱ)求证：f(x)在R上是单调增函数；
(Ⅲ)若a＞b＞c＞0，且b2=ac，求证：f(a)+f(c)＞2(b)。
①对任意x∈R，有f(x)＞0；
②对任意x，y∈R，有f(xy)=[f(x)]y；
③
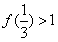；(Ⅰ)求f(0)的值；
(Ⅱ)求证：f(x)在R上是单调增函数；
(Ⅲ)若a＞b＞c＞0，且b2=ac，求证：f(a)+f(c)＞2(b)。
(Ⅰ)解：令x=0，y=2，得f(0)=[f(0)]2，
∵f(0)＞0，
∴f(0)=1．
(Ⅱ)证明：任取x1，x2∈(-∞，+∞)，且x1＜x2，
设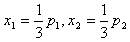
，
则p1＜p2，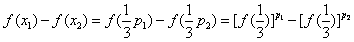
，
，p1＜p2，
∴f(x1)＜f(x2)，
∴f(x)在R上是单调增函数．
(Ⅲ)证明：由(Ⅰ)(Ⅱ)知f(b)＞f(0)=1，
∴f(b)＞1，
，
，
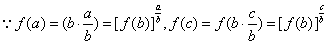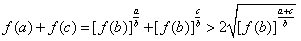而
，
∴
，
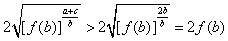∴f(a)+f(c)＞2f(b)。
∵f(0)＞0，
∴f(0)=1．
(Ⅱ)证明：任取x1，x2∈(-∞，+∞)，且x1＜x2，
设
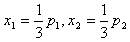，则p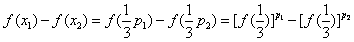1＜p2，
，，p1＜p2，∴f(x1)＜f(x2)，
∴f(x)在R上是单调增函数．
(Ⅲ)证明：由(Ⅰ)(Ⅱ)知f(b)＞f(0)=1，
∴f(b)＞1，
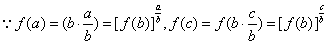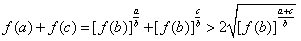，，而
，∴
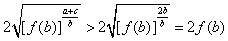，∴f(a)+f(c)＞2f(b)。
练习册系列答案
学业测评一课一测系列答案
小学课时作业全通练案系列答案
相关题目
的定义域为R,则k的取值范围为___________. 
的定义域是一切实数,则m的取值范围是( )