题目内容
给出下列说法:
(1)函数y=
与y=x
是同一函数;
(2)f(x)=x+
,(x∈(0,1))的值域为(3,+∞);
(3)若函数f(x)的定义域为[0,2],则函数g(x)=
的定义域为[0,2);
(4)集合{x∈N|x=
,a∈N *}中只有四个元素;其中正确的是
(1)函数y=
| -2x 3 |
| -2x |
(2)f(x)=x+
| 2 |
| x |
(3)若函数f(x)的定义域为[0,2],则函数g(x)=
| f(2x) |
| x-2 |
(4)集合{x∈N|x=
| 6 |
| a |
(2)(4)
(2)(4)
(只写番号).分析:对于(1)由于函数y=
=-x
,从而得出结论;(2)利用f(x)=x+
在(0,1)上是单调减函数即可进行判断;对于(3)若函数f(x)的定义域为[0,2],则由
求出函数g(x)的定义域即可进行判断;(4)化简集合{x∈N|x=
,a∈N *}={6,3,2,1},其中只有四个元素,正确.
| -2x 3 |
| -2x |
| 2 |
| x |
|
| 6 |
| a |
解答:解:(1)由于函数y=
=-x
,故函数y=
与y=x
不是同一函数,故(1)错;
(2)∵f(x)=x+
在(0,1)上是单调减函数,且当x→0时,y→+∞,当x→1时,y→3,
∴f(x)=x+
在x∈(0,1)的值域为(3,+∞)正确;
(3)若函数f(x)的定义域为[0,2],则由
,得0≤x≤1,
∴函数g(x)的定义域为[0,1],故(3)错.
(4)集合{x∈N|x=
,a∈N *}={6,3,2,1},其中只有四个元素;正确.
其中正确的是 (2)(4).
故答案为:(2)(4).
| -2x 3 |
| -2x |
| -2x 3 |
| -2x |
(2)∵f(x)=x+
| 2 |
| x |
∴f(x)=x+
| 2 |
| x |
(3)若函数f(x)的定义域为[0,2],则由
|
∴函数g(x)的定义域为[0,1],故(3)错.
(4)集合{x∈N|x=
| 6 |
| a |
其中正确的是 (2)(4).
故答案为:(2)(4).
点评:本小题主要考查函数单调性的应用、函数的定义域及其求法、判断两个函数是否为同一函数等基础知识,考查运算求解能力,考查转化思想.属于基础题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
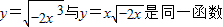 ;
;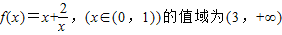 ;
; ;
;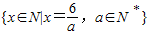 中只有四个元素;其中正确的是 (只写番号).
中只有四个元素;其中正确的是 (只写番号).