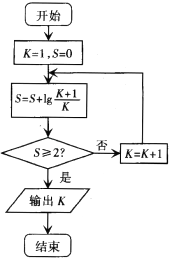
题目内容
【题目】已知f（x）=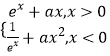 
，若函数f（x）有四个零点，则实数a的取值范围是（ ）
A.（﹣∞，﹣e）
B.（﹣∞，﹣ 
）
C.（﹣∞，﹣ 
）
D.（﹣∞，﹣ 
）
【答案】B
【解析】解：由函数f（x）为偶函数，可知使函数f（x）有四个零点， 只需要ex+ax2=0有两个正根，
即﹣ 
=a有两个正根，
设g（x）=﹣ ，求导g′（x）=﹣ 
=﹣ 
，
令g′（x）＞0，解得：0＜x＜2，g（x）在（0，2）单调递增，
令g′（x）＜0，解得：x＞2，g（x）在（2，+∞）单调递减，
∴g（x）在x=2时取最大值，最大值g（2）=﹣ 
，
要使﹣ =a有两个正根，即使g（x）与y=a有两个交点，
∴实数a的取值范围（﹣∞，﹣ ），
故选B．
练习册系列答案
阅读快车系列答案
相关题目
【题目】甲、乙两人玩一种游戏，游戏规则如下：先将筹码放在如下表的正中间D处，投掷一枚质地均匀的硬币，若正面朝上，筹码向右移动一格；若反面朝上，筹码向左移动一格．
A | B | C | D | E | F | G |
30 | 5 | 10 | 10 | 5 | 20 | 30 |
（1）将硬币连续投掷三次，现约定：若筹码停在A或B或C或D处，则甲赢；否则，乙赢．问该约定对乙公平吗？请说明理由．
（2）设甲、乙两人各有100个积分，筹码停在D处，现约定： ①投掷一次硬币，甲付给乙10个积分；乙付给甲的积分数是，按照上述游戏规则筹码所在表中字母A﹣G下方所对应的数目；
②每次游戏筹码都连续走三步，之后重新回到起始位置D处．
你认为该规定对甲、乙二人哪一个有利，请说明理由．
