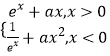题目内容
【题目】已知数列{an}的前n项和 
，数列{bn}的前n项和为Bn ．
（1）求数列{an}的通项公式；
（2）设 
，求数列{cn}的前n项和Cn；
（3）证明： 
．
【答案】
（1）解：当n≥2时， 
， 
，
两式相减：an=An﹣An﹣1=2n﹣1；
当n=1时，a1=A1=1，也适合an=2n﹣1，
故数列{an}的通项公式为an=2n﹣1
（2）解：由题意知： 
，Cn=c1+c2+…+cn，
， 
，
两式相减可得： 
，
即 
， 
， 
（3）解： 
，显然 
，
即bn＞2，Bn=b1+b2+…+bn＞2n
另一方面， 
，
即 
， 
， 
， 
，
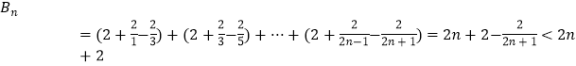即：2n＜Bn＜2n+2
【解析】（1）当n≥2时，利用an=An﹣An﹣1可得an=2n﹣1，再验证n=1的情况，即可求得数列{an}的通项公式；（2）由题意知： ，利用错位相减法即可求得数列{cn}的前n项和Cn；（3）利用基本不等式可得 ＞ 
，可得Bn=b1+b2+…+bn＞2n；再由bn= ，累加可 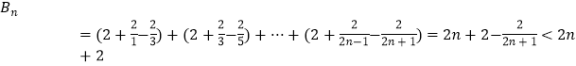， 于是可证明： 
．
【考点精析】关于本题考查的数列的通项公式，需要了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能得出正确答案．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
