题目内容
若函数y=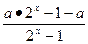 为奇函数,
为奇函数,
(1)确定a的值;
(2)求函数的定义域;
(3)求函数的值域;
(4)讨论函数的单调性.
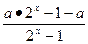 为奇函数,
为奇函数,(1)确定a的值;
(2)求函数的定义域;
(3)求函数的值域;
(4)讨论函数的单调性.
(1)由奇函数的定义,可得f(-x)+f(x)=0,即a-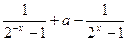 =0,
=0,
∴2a+ =0.
=0.
∴a=- .
.
(2)∵y=- -
- ,
,
∴2x-1≠0.
∴函数y=- -
- 的定义域为{x|x≠0}.
的定义域为{x|x≠0}.
(3)方法一:(逐步求解法)
∵x≠0,
∴2x-1>-1.
∵2x-1≠0,
∴0>2x-1>-1或2x-1>0.
∴- -
- >
> ,-
,- -
- <-
<- ,
,
即函数的值域为{y|y> 或y<-
或y<- }.
}.
方法二:(利用有界性)由y=- -
- ≠-
≠- ,可得2x=
,可得2x= .
.
∵2x>0,∴ >0.可得y>
>0.可得y> 或y<-
或y<- ,
,
即函数的值域为{y|y> 或y<-
或y<- }.
}.
(4)当x>0时,设0<x1<x2,则y1-y2= .
.
∵0<x1<x2,
∴1< <
<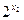 .
.
∴ -
-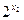 <0,
<0, -1>0,
-1>0,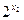 -1>0.
-1>0.
∴y1-y2<0.
因此y=- -
- 在(0,+∞)上递增.
在(0,+∞)上递增.
同样可以得出y=- -
- 在(-∞,0)上递增.
在(-∞,0)上递增.
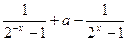 =0,
=0,∴2a+
 =0.
=0.∴a=-
 .
.(2)∵y=-
 -
- ,
,∴2x-1≠0.
∴函数y=-
 -
- 的定义域为{x|x≠0}.
的定义域为{x|x≠0}.(3)方法一:(逐步求解法)
∵x≠0,
∴2x-1>-1.
∵2x-1≠0,
∴0>2x-1>-1或2x-1>0.
∴-
 -
- >
> ,-
,- -
- <-
<- ,
,即函数的值域为{y|y>
 或y<-
或y<- }.
}.方法二:(利用有界性)由y=-
 -
- ≠-
≠- ,可得2x=
,可得2x= .
.∵2x>0,∴
 >0.可得y>
>0.可得y> 或y<-
或y<- ,
,即函数的值域为{y|y>
 或y<-
或y<- }.
}.(4)当x>0时,设0<x1<x2,则y1-y2=
 .
.∵0<x1<x2,
∴1<
 <
<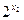 .
.∴
 -
-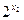 <0,
<0, -1>0,
-1>0,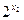 -1>0.
-1>0.∴y1-y2<0.
因此y=-
 -
- 在(0,+∞)上递增.
在(0,+∞)上递增.同样可以得出y=-
 -
- 在(-∞,0)上递增.
在(-∞,0)上递增.先将函数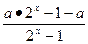 化简为y=a-
化简为y=a- .
.
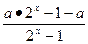 化简为y=a-
化简为y=a- .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
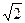 ,b="2"
,b="2" ,b=(2x)2,c=
,b=(2x)2,c=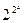 ,则a、b、c的大小关系是( )
,则a、b、c的大小关系是( )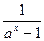 +
+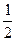 )x,
)x, 在
在 上的值域。
上的值域。 的图像不经过第二象限,则
的图像不经过第二象限,则 的取值范围是 ( )
的取值范围是 ( )




 是奇函数,满足
是奇函数,满足 ,当
,当 时,
时, ,则
,则 .
.