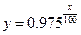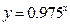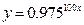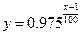题目内容
设a>1，函数f(x)=(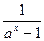
+
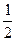)x,
(1)判断函数的奇偶性;
(2)求证：对于x≠0,f(x)>0.
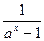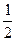+)x,(1)判断函数的奇偶性;
(2)求证：对于x≠0,f(x)>0.
(2)证明:x>0时,∵a>1ax>1,易证f(x)>0,而x<0时,由f(x)=f(-x)>0,故对于x≠0,f(x)>0.(1)f(x)为定义域上的增函数.
(2)证明:x>0时,∵a>1ax>1,易证f(x)>0,而x<0时,由f(x)=f(-x)>0,故对于x≠0,f(x)>0.
(2)证明:x>0时,∵a>1ax>1,易证f(x)>0,而x<0时,由f(x)=f(-x)>0,故对于x≠0,f(x)>0.
(1)由题意得函数f(x)=(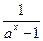
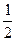+)x的定义域为x∈（-∞,0）∪（0,+∞）.?
对于定义域内任意x，有?
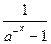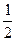f(-x)="("
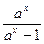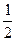+)(-x)?
=(
-)x?
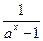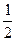=(+)x=f(x),?
∴f(x)为定义域上的增函数.
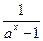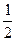+)x的定义域为x∈（-∞,0）∪（0,+∞）.?对于定义域内任意x，有?
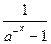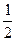f(-x)="("
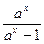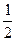+)(-x)?=(
-)x?=(
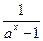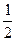+)x=f(x),?∴f(x)为定义域上的增函数.
练习册系列答案
相关题目
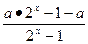为奇函数，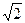
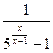的定义域为__________________.
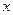年后的剩留量为
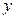，则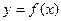
的函数解析式为 （ ）
