题目内容

8．若方程x2+y2-2x+4y+m=0表示一个圆，则此圆的圆心坐标为（-1，2），m的取值范围是（-∞，5）．

分析 把圆的方程化为圆的标准方程，可得圆心的坐标；再根据圆的标准方程，求出m的范围．

解答 解：方程x2+y2-2x+4y+m=0表示一个圆，此圆即（x-1）2+（y+2）2 =5-m，
则此圆的圆心坐标为（1，-2）．
由5-m＞0，可得m＜5，
故答案为：（1，-2）；（-∞，5）．

点评 本题主要考查圆的标准方程的特征，属于基础题．

练习册系列答案
相关题目
18．已知A（3，-4），B（6，-3），C（m+5，m-3）三点能确定三角形，那么实数m的取值范围是m≠-$\frac{1}{2}$．
19．某商场节日期间做有奖促销活动，在一个大盒子里装有10只乒乓球，其中有2只黄球，8只白球，任取2只，如果2只都是黄球中一等奖，有1只黄球中二等奖，都是白球不获奖，试求：
（1）取到黄球个数X的分布列；
（2）某顾客中奖的概率．
16．函数y=$\sqrt{{x^2}-8x+20}$+$\sqrt{{x^2}+1}$的最小值为（　　）
A．12B．25C．8D．5
3．等差数列{an}的前n项和为Sn，若a1=1，S4=S9，则S12=1．
13．在由数字1，2，3，4，5组成的可重复数字的三位数中，如：213，212，222等表示的数中，只有1个偶数“2”，我们称这样的数只有一个偶数数字，从这样的三位数中任取一个数，则该数是没有重复数字 的三位数的概率为$\frac{18}{37}$．
20．${（\sqrt{x}-\frac{2}{x}）^n}$的展开式中的第5项是常数项，则n=12．
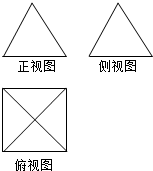17．若一个四梭锥的三视图如图所示，其中正视图与侧视图都是边长为2的等边三角形，则该四棱锥的四条侧棱长之和等于4$\sqrt{5}$．
18．定义在R上的奇函数f（x），对任意x∈R都有f（x+2）=f（-x），当x∈（0，2）时，f（x）=4x，则f（2015）=-4．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网