题目内容
设函数f(x)=x+ax2+blnx,曲线y=f(x)过P(1,0),且在P点处的切线斜率为2.
(1)求a,b的值;
(2)证明:f(x)≤2x-2.
【答案】
(1) a=-1,b=3. (2)利用导数证明。
【解析】
试题分析: (1)f
′(x)=1+2ax+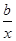 .(1分)
.(1分)
由已知条件得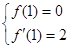 即
即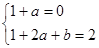
解得a=-1,b=3. (4分)
(2)f(x)的定义域为(0,+∞),
由(1)知f(x)=x-x2+3lnx.
设g(x)=f(x)-(2x-2)=2-x-x2+3lnx,则
g′(x)=-1-2x+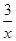 =-
=-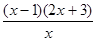 . (6分)
. (6分)
当0<x<1时,g′(x)>0;当x>1时,g′(x)<0.
所以g(x)在(0,1)单调递增,在(1,+∞)单调递减.(8分)
而g(1)=0,故当x>0时,g(x)≤0,即f(x)≤2x-2. (10分)
考点:本题主要考查导数的几何意义,利用导数研究函数的单调性、最值,不等式组的证明。
点评:中档题,导数的应用是高考必考内容,思路往往比较明确根据导数值的正负,确定函数的单调性。定义不懂事的证明问题,往往通过构造函数,转化成求函数的最值,使问题得解。

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
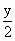 )是函数y=g(x)图象上的点.
)是函数y=g(x)图象上的点. ,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.
,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.