题目内容
设函数f(x)= ,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.
,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.
【答案】
2
【解析】
试题分析:当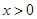 时,
时,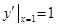 ,所以该曲线在点(1,0)处的切线方程为
,所以该曲线在点(1,0)处的切线方程为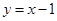 ,画出可行域,在画出目标函数z=x-2y,可知在
,画出可行域,在画出目标函数z=x-2y,可知在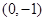 处取到最大值,最大值为2.
处取到最大值,最大值为2.
考点:本小题主要考查导数几何意义的应用和由线性规划知识解决最值问题,考查学生的运算求解能力和数形结合思想的应用.
点评:解决线性规划问题的关键是正确画出可行域.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
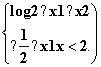 若f(x0)>1,则x0的取值范围是( )
若f(x0)>1,则x0的取值范围是( )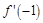 的取值范围是( ▲ )
的取值范围是( ▲ )