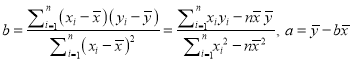题目内容
【题目】一次函数f(x)是R上的增函数,已知f[f(x)]=16x+5,g(x)=f(x)(x+m).
(1)求f(x);
(2)若g(x)在(1,+∞)单调递增,求实数m的取值范围;
(3)当x∈[﹣1,3]时,g(x)有最大值13,求实数m的值.
【答案】
(1)解:∵f(x)是R上的增函数,
∴设f(x)=ax+b,a>0,
f[f(x)]=a(ax+b)+b=a2x+ab+b=16x+5,
∴a2=16,ab+b=5,
解得a=4,b=1或a=﹣4,b=﹣ ![]() (不合题意舍去),
(不合题意舍去),
∴f(x)=4x+1
(2)解:g(x)=f(x)(x+m)=(4x+1)(x+m)=4x2+(4m+1)x+m,
对称轴为x=﹣ ![]() ,
,
由题意可得﹣ ![]() ≤1,解得m≥﹣
≤1,解得m≥﹣ ![]()
(3)解:由于g(x)为开口向上的抛物线,
可得g(x)的最大值为端点处的函数值.
当g(﹣1)取得最大值时,即﹣3(m﹣1)=13,解得m=﹣ ![]() ;
;
当g(3)取得最大值时,即13(m+3)=13,解得m=﹣2.
当m=﹣2时,对称轴为x=﹣ ![]() =
= ![]() ,g(﹣1)=9<g(3)=13;
,g(﹣1)=9<g(3)=13;
当m=﹣ ![]() 时,对称轴为x=﹣
时,对称轴为x=﹣ ![]() =
= ![]() ,g(﹣1)=13>g(3)=﹣13.
,g(﹣1)=13>g(3)=﹣13.
综上可得,m=﹣2或﹣ ![]()
【解析】(1)设f(x)=ax+b,a>0,代入条件,由恒等式的性质可得方程,解方程可得f(x)的解析式;(2)求得g(x)的解析式和对称轴方程,再由单调性可得﹣ ![]() ≤1,解不等式即可得到所求范围;(3)根据抛物线的开口向上,可得最大值在端点处取得,解方程可得m的值,注意检验即可得到.
≤1,解不等式即可得到所求范围;(3)根据抛物线的开口向上,可得最大值在端点处取得,解方程可得m的值,注意检验即可得到.
【考点精析】解答此题的关键在于理解函数单调性的性质的相关知识,掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集,以及对函数的最值及其几何意义的理解,了解利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.

【题目】(本小题满分12分)
微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有![]() ﹪的把握认为“微信控”与“性别”有关?
﹪的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5人中再随机抽取3人赠送200元的护肤品套装,记这3人中“微信控”的人数为![]() ,试求
,试求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式: 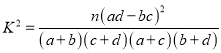 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差x/摄氏度 | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再用被选取的2组数据进行检验。
(Ⅰ)求选取的2组数据恰好是不相邻2天的数据的概率;
(Ⅱ)若选取的是12月1日与12月5日的2组数据,请根据12月2日至4日的数据,求出y关于x的线性回归方程![]() ,并判断该线性回归方程是否可靠(若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的
,并判断该线性回归方程是否可靠(若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: