题目内容
定义在(0,+∞)上的三个函数f(x)、g(x)、h(x),已知f(x)=lnx,g(x)=x2-af(x),h(x)=x-a| x |
(1)求a的值及h(x)的单调区间;
(2)求证:当1<x<e2时,恒有x<
| 2+f(x) |
| 2-f(x) |
(3)把h(x)对应的曲线C1向上平移6个单位后得到曲线C2,求C2与g(x)对应曲线C3的交点的个数,并说明道理.
分析:(1)表示出函数g(x)后对其进行求导,将x=1代入导数g'(x)即可得到答案.
(2)欲证:x<
.只需证:x[2-f(x)]<2+f(x),即证:f(x)>
.
(3)表示出C2的解析式,h1(x),转化为求h1(x)与g(x)的交点个数即可.
(2)欲证:x<
| 2+f(x) |
| 2-f(x) |
| 2(x-1) |
| x+1 |
(3)表示出C2的解析式,h1(x),转化为求h1(x)与g(x)的交点个数即可.
解答:解:(1)由题意:g(x)=x2-af(x)=x2-alnx
g'(1)=2-a=0,∴a=2
而h(x)=x-2
,h'(x)=1-
,
令h'(x)=1-
>0 得 x>1,所以 h(x)在(1,+∞)上位增函数
令h'(x)=1-
<0 得 0<x<1,h(x)在(0,1)上为减函数.
(2)∵1<x<e2∴0<lnx<2,∴2-lnx>0,
欲证:x<
.只需证:x[2-f(x)]<2+f(x),即证:f(x)>
记k(x)=f(x)-
=lnx-
∴k'(x)=
∴当x>1时,k'(x)>0∴k(x)在[1,+∞)上为增函数
∴k(x)>k(1)=0,∴k(x)>0
即lnx-
>0,∴lnx>
∴结论成立
 (3)由(1)知:g(x)=x2-2lnx,h(x)=x-2
(3)由(1)知:g(x)=x2-2lnx,h(x)=x-2
∴C2对应表达式为h1(x)=x-2
+6
∴问题转化为求函数g(x)=x2-2lnx与h1(x)=x-2
+6交点的个数
即方程:x2-2lnx=x-2
+6的根的个数
即:2
-2lnx=-x2+x+6
设h2 (x)=2
-2lnx,h3(x)=-x2+x+6,
(x)=
-
=
=
∴当x∈(0,4)时,h2′(x)<0,h2(x)为减函数
当x∈(4,+∞)时,h2′(x)>0,h2(x)为增函数
而h3(x)=-x2+x+6的图象开口向下的抛物线
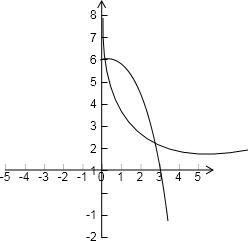
∴h3(x)与h2(x)的大致图象如图:
∴h3(x)与h2(x)的交点个数为2个,即C2与C3的交点个数为2个.
g'(1)=2-a=0,∴a=2
而h(x)=x-2
| x |
| 1 | ||
|
令h'(x)=1-
| 1 | ||
|
令h'(x)=1-
| 1 | ||
|
(2)∵1<x<e2∴0<lnx<2,∴2-lnx>0,
欲证:x<
| 2+f(x) |
| 2-f(x) |
| 2(x-1) |
| x+1 |
记k(x)=f(x)-
| 2(x-1) |
| x+1 |
| 2(x-1) |
| x+1 |
∴k'(x)=
| (x-1)2 |
| x(x+1)2 |
∴当x>1时,k'(x)>0∴k(x)在[1,+∞)上为增函数
∴k(x)>k(1)=0,∴k(x)>0
即lnx-
| 2(x-1) |
| x+1 |
| 2(x-1) |
| x+1 |
∴结论成立
 (3)由(1)知:g(x)=x2-2lnx,h(x)=x-2
(3)由(1)知:g(x)=x2-2lnx,h(x)=x-2| x |
∴C2对应表达式为h1(x)=x-2
| x |
∴问题转化为求函数g(x)=x2-2lnx与h1(x)=x-2
| x |
即方程:x2-2lnx=x-2
| x |
即:2
| x |
设h2 (x)=2
| x |
| h | ′ 2 |
| 1 | ||
|
| 2 |
| x |
| ||||
x
|
| ||
| x |
∴当x∈(0,4)时,h2′(x)<0,h2(x)为减函数
当x∈(4,+∞)时,h2′(x)>0,h2(x)为增函数
而h3(x)=-x2+x+6的图象开口向下的抛物线
∴h3(x)与h2(x)的大致图象如图:
∴h3(x)与h2(x)的交点个数为2个,即C2与C3的交点个数为2个.
点评:本题主要考查通过求函数的导数来确定函数的增减区间的问题.这里要熟记各种函数的求导法则.

练习册系列答案
相关题目
已知定义在(0,1)上的函数f(x),对任意的m,n∈(1,+∞)且m<n时,都有f(
)-f(
)=f(
)记an=f(
),n∈N*,则在数列{an}中,a1+a2+…a8=( )
| 1 |
| n |
| 1 |
| m |
| m-n |
| 1-mn |
| 1 |
| n2+5n+5 |
A、f(
| ||
B、f(
| ||
C、f(
| ||
D、f(
|