题目内容
(1)计算:2log52+log5
+loge
+3
×
×21-log23;
(2)求函数f(x)=
的定义域.
| 5 |
| 4 |
| e |
| 1 |
| 2 |
|
(2)求函数f(x)=
| 3-log2x |
分析:(1)把同底数第一、二项利用对数的运算法则进行计算,第四项根据对数恒等式及指数去处法则可求,化简求值即可;
(2)根据负数没有平方根得到被开方式大于等于0,又根据负数和0没有对数得到x大于0,被开方式大于等于0列出的不等式移项并根据对数的运算性质变形后,由3大于1时,对数函数为增函数,得到x的范围,与x大于0求出交集即为函数f(x)的定义域.
(2)根据负数没有平方根得到被开方式大于等于0,又根据负数和0没有对数得到x大于0,被开方式大于等于0列出的不等式移项并根据对数的运算性质变形后,由3大于1时,对数函数为增函数,得到x的范围,与x大于0求出交集即为函数f(x)的定义域.
解答:解:(1)原式=log522+log5
+logee
+3
×(
)
×(2 ÷2log23)(3分)
=log5(4×
)+
+
×(2÷3)(6分)
=1+
+1=
(7分)
(2):3-log2x≥0且 x>0(2分)
log2x≤3=log223且 x>0(3分)
log2x≤log28且 x>0(4分),
∴0<x≤8.
则函数f(x)的定义域为:(0,8].(缺x>0给3分)
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
=log5(4×
| 5 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
=1+
| 1 |
| 2 |
| 5 |
| 2 |
(2):3-log2x≥0且 x>0(2分)
log2x≤3=log223且 x>0(3分)
log2x≤log28且 x>0(4分),
∴0<x≤8.
则函数f(x)的定义域为:(0,8].(缺x>0给3分)
点评:本题考查了对数函数的定义域、有理数指数幂的化简求值和对数的基本运算、对数的运算法则,应熟练掌握分数指数幂和对数的运算性质,属基础题.

练习册系列答案
相关题目
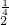
 -1)0+(
-1)0+( )
)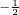 +(
+( )
)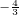 .
.