题目内容
计算:(1)(| 7 |
| 6 |
| 7 |
| 6 |
| 10 |
(2)log2(1+
| 2 |
| 3 |
| 2 |
| 3 |
分析:(1)利用
+
与
-
互为倒数,对数恒等式及对数的运算性质,运算求得结果.
(2)直接利用对数的运算性质,把要求的式子化为=log2(1+
+
)(1+
-
)=log2(2
)
=log22
,从而得到答案.
| 7 |
| 6 |
| 7 |
| 6 |
(2)直接利用对数的运算性质,把要求的式子化为=log2(1+
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
=log22
| 3 |
| 2 |
解答:解:(1)(
+
)2log(
-
)
=(
+
)log(
-
)10=(
-
)-log(
-
)10
=(
-
)log(
-
)
=
,故答案为:
.
(2)log2(1+
+
)+log2(1+
-
)=log2(1+
+
)(1+
-
)=log2(2
)
=log22
=
,
故答案为:
.
| 7 |
| 6 |
| 7 |
| 6 |
| 10 |
| 7 |
| 6 |
| 7 |
| 6 |
| 7 |
| 6 |
| 7 |
| 6 |
=(
| 7 |
| 6 |
| 7 |
| 6 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
(2)log2(1+
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
=log22
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查对数恒等式,对数的运算性质的应用,式子的变形是解题的难点.

练习册系列答案
相关题目
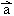 =-42
=-42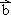 )-8
)-8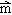 +
+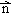 ,
,