题目内容
设数列{an}的前n项和为Sn,且Sn=(λ+1)-λan,其中λ是不等于-1和0的常数.(Ⅰ)证明an是等比数列;
(Ⅱ)设数列{an}的公比q=f(λ),数列{bn}满足
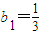 ,bn=f(bn-1)(n∈N,n≥2),求数列
,bn=f(bn-1)(n∈N,n≥2),求数列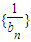 的前n项和为Tn.
的前n项和为Tn.
【答案】分析:(Ⅰ)由an=Sn-Sn-1=(λ+1)-λan -[(λ+1)-λan-1 ],得到an和an-1的关系式.再由等比数列的定义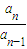 为常数得证.
为常数得证.
(Ⅱ)由(Ⅰ)得,bn和bn-1之间的关系.即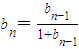 ,两边取倒数,构造了
,两边取倒数,构造了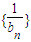 这个等差数列.再根据公式求和.
这个等差数列.再根据公式求和.
解答:解:(Ⅰ)∵Sn=(λ+1)-λan∴Sn-1=(λ+1)-λan-1(n≥2)
∴an=-λan+λan-1即(1+λ)an=λan-1又λ≠-1且λ≠0
∴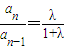 又a1=1
又a1=1
∴an是以1为首项,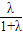 为公比的等比数列
为公比的等比数列
(Ⅱ)由(Ⅰ)知:q=f(λ)=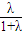
∴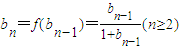 故有
故有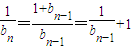 ∴
∴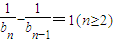
∴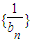 是以3为首项,1为公差的等差数列
是以3为首项,1为公差的等差数列
∴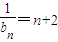
∴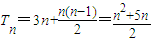
点评:对于数列的题目,迭代的思想是最常用的方法,另外,已知递推关系式,求通项公式也是常见的题型,比如,构造等差数列,构造等比数列等.
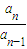 为常数得证.
为常数得证.(Ⅱ)由(Ⅰ)得,bn和bn-1之间的关系.即
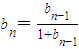 ,两边取倒数,构造了
,两边取倒数,构造了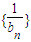 这个等差数列.再根据公式求和.
这个等差数列.再根据公式求和.解答:解:(Ⅰ)∵Sn=(λ+1)-λan∴Sn-1=(λ+1)-λan-1(n≥2)
∴an=-λan+λan-1即(1+λ)an=λan-1又λ≠-1且λ≠0
∴
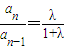 又a1=1
又a1=1∴an是以1为首项,
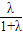 为公比的等比数列
为公比的等比数列(Ⅱ)由(Ⅰ)知:q=f(λ)=
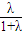
∴
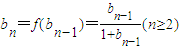 故有
故有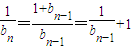 ∴
∴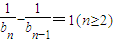
∴
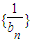 是以3为首项,1为公差的等差数列
是以3为首项,1为公差的等差数列∴
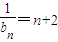
∴
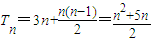
点评:对于数列的题目,迭代的思想是最常用的方法,另外,已知递推关系式,求通项公式也是常见的题型,比如,构造等差数列,构造等比数列等.

练习册系列答案
相关题目