题目内容
设曲线 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为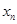 ,则
,则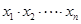 的值为( )
的值为( )
A.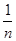 | B.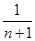 | C.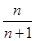 | D.1 |
B
解析试题分析:因为, ,所以,
,所以,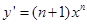 ,曲线
,曲线 在点(1,1)处的切线斜率为n+1,切线方程为
在点(1,1)处的切线斜率为n+1,切线方程为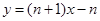 ,令y=0得,x=
,令y=0得,x=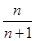 ,即
,即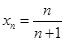 ,
,
所以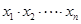
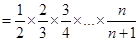 =
=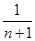 。选B。
。选B。
考点:本题主要考查导数的几何意义,直线方程,等比数列的求和公式。
点评:中档题,切线的斜率等于函数在切点的导函数值。最终转化成确定数列的通项公式问题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
曲线C:y=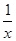 ,则x轴与C及直线x=1、x=2围成的封闭图形的面积为
,则x轴与C及直线x=1、x=2围成的封闭图形的面积为
| A.1n2一1 | B.1一1n2 | C.1n2 | D.2-1n2 |
已知函数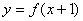 的图象关于点
的图象关于点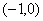 对称,且当
对称,且当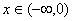 时,
时,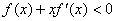 成立(其中
成立(其中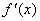 是
是 的导函数),若
的导函数),若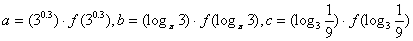 ,则a,b,c的大小关系为( )
,则a,b,c的大小关系为( )
| A.a > c >b | B.c>a>b | C.c> b > a | D.b >a> c |
如图,函数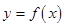 的图象在点P处的切线方程是
的图象在点P处的切线方程是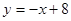 ,则
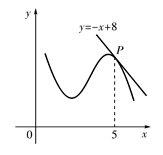
,则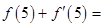 ( )
( )
A.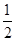 | B. | C.2 | D.0 |
过点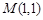 且与曲线
且与曲线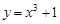 相切的直线方程是( )
相切的直线方程是( )
A.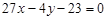 |
B.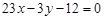 或 或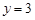 |
C.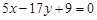 |
D.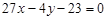 或 或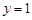 |
已知函数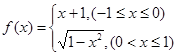 , 则
, 则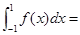 ( )
( )
A. | B.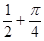 | C.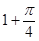 | D.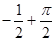 |
已知二次函数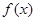 =
=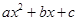 的导数为
的导数为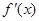 ,
, >0,对任意实数
>0,对任意实数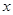 都有
都有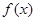 ≥0,则
≥0,则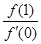 的最小值为( )
的最小值为( )
| A.4 | B.3 | C.8 | D.2 |
在 上可导的函数
上可导的函数 ,当
,当 时取得极大值,当
时取得极大值,当 时取得极小值,则
时取得极小值,则 的取值范围是( )
的取值范围是( )
A.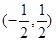 | B. | C. | D.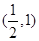 |
函数 在点
在点 处的导数是
处的导数是
A. | B. | C. | D. |