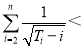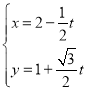题目内容
【题目】已知![]() 是椭圆
是椭圆![]() :
:![]() 上一点,以点
上一点,以点![]() 及椭圆的左、右焦点
及椭圆的左、右焦点![]() ,
,![]() 为顶点的三角形面积为
为顶点的三角形面积为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作斜率存在且互相垂直的直线
作斜率存在且互相垂直的直线![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 两交点的中点,
两交点的中点,![]() 是
是![]() 与
与![]() 两交点的中点,求△
两交点的中点,求△![]() 面积的最大值.
面积的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)通过已知建立方程组,解方程组即得椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设直线![]() :
:![]() ,联立直线和椭圆方程得到韦达定理,求出
,联立直线和椭圆方程得到韦达定理,求出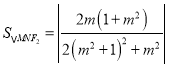 ,令
,令![]() ,
,![]() ,则
,则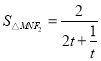 再利用导数求函数的最大值得解.
再利用导数求函数的最大值得解.
解:(Ⅰ)由点![]() 在椭圆上可得
在椭圆上可得![]() ,
,
整理得![]() ①.
①.
![]() ,解得
,解得![]() ,
,
所以![]() ,代入①式整理得
,代入①式整理得![]() ,
,
解得![]() ,
,![]() .
.
所以椭圆的标准方程为![]() .
.
(Ⅱ)由(Ⅰ)可得![]() ,所以设直线
,所以设直线![]() :
:![]() ,
,
联立直线与椭圆的方程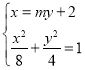 ,整理得
,整理得![]() .
.
所以直线![]() 与椭圆两交点的中点
与椭圆两交点的中点![]() 的纵坐标
的纵坐标![]() ,
,
同理直线![]() 与椭圆两交点的中点
与椭圆两交点的中点![]() 的纵坐标
的纵坐标 ,
,
所以![]()
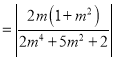
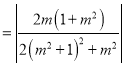 ,
,
将上式分子分母同除![]() 可得,
可得,
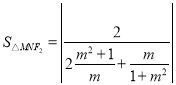 ,
,
不妨设![]() ,令
,令![]() ,
,![]() ,则
,则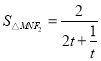 ,
,
令![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 单调递增,
单调递增,
所以当![]() 时,三角形△
时,三角形△![]() 面积取得最大值
面积取得最大值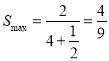 .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目