题目内容
已知函数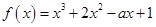 在区间
在区间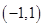 上恰有一个极值点,则实数
上恰有一个极值点,则实数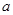 的取值范围是
的取值范围是
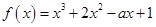 在区间
在区间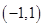 上恰有一个极值点,则实数
上恰有一个极值点,则实数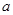 的取值范围是
的取值范围是 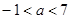 .
.试题分析:首先利用函数的导数与极值的关系求出
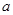 的值,由于函数
的值,由于函数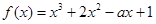 在区间
在区间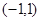 上恰有一个极值点,所以
上恰有一个极值点,所以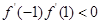 ,故可求得
,故可求得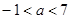 ,.
,.点评:考查利用导数研究函数的极值问题,体现了数形结合和转化的思想方法.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
题目内容
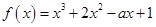 在区间
在区间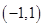 上恰有一个极值点,则实数
上恰有一个极值点,则实数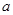 的取值范围是
的取值范围是 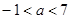 .
.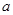 的值,由于函数
的值,由于函数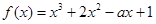 在区间
在区间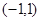 上恰有一个极值点,所以
上恰有一个极值点,所以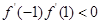 ,故可求得
,故可求得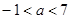 ,.
,.
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案