题目内容
(本小题满分12分)
已知函数f(x)=2sinxcosx+cos2x.
(1)求 的值;
的值;
(2)求函数f(x)的最大值及取得最大值时x的值。
(1)1(2)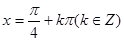 ,最大值为
,最大值为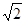
解析试题分析:解(1)∵f(x)=sin2x+cos2x,∴f(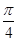 )=sin
)=sin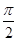 +cos
+cos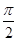 ="1"
="1"
(2)f(x)=sin2x+cos2x=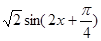 所以最大值为
所以最大值为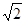
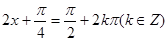 所以
所以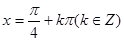
考点:三角函数的性质
点评:解决的关键是利用三角函数的两角和差公式变形,然后结合正弦函数性质得到结论,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
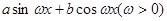 的周期为
的周期为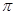 ,且对一切x
,且对一切x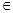 R,都有f(x)
R,都有f(x)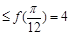 ;
; 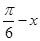 ),求函数g(x)的单调增区间;
),求函数g(x)的单调增区间;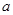 ,使得函数
,使得函数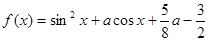 在闭区间
在闭区间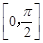 上的最大值为1?若存在,求出对应的
上的最大值为1?若存在,求出对应的 ,
,
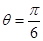 时,求
时,求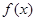 的最大值和最小值
的最大值和最小值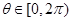 ,求
,求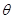 的取值范围。
的取值范围。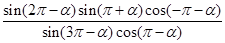
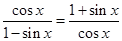
 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 .
. 的值;
的值; 求
求 的取值范围。
的取值范围。 ,
,
 时,求
时,求 的最大值和最小值
的最大值和最小值
 ,求
,求 的取值范围
的取值范围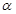 是第二象限角,且
是第二象限角,且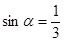 求
求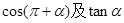 的值;
的值;

 ,
, 的最小值是
的最小值是 ,最大值是
,最大值是 ,求实数
,求实数 的值.
的值.