题目内容
已知函数 ,
,
(1)当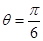 时,求
时,求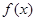 的最大值和最小值
的最大值和最小值
(2)若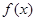 在
在 上是单调函数,且
上是单调函数,且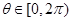 ,求
,求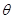 的取值范围。
的取值范围。
(1)当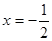 时,函数
时,函数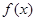 有最小值
有最小值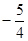 ,当
,当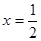 时,函数
时,函数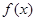 有最小值
有最小值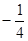 .
.
(2)
解析试题分析:(1)当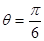 时,
时,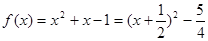
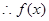 在
在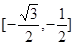 上单调递减,在
上单调递减,在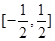 上单调递增
上单调递增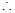 当
当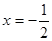 时,函数
时,函数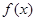 有最小值
有最小值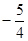
当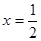 时,函数
时,函数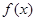 有最小值
有最小值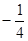
(2)要使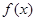 在
在 上是单调函数,则
上是单调函数,则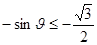 或
或
即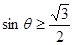 或
或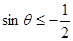
又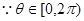
解得:
考点:本题主要考查正弦函数的图象和性质,二次函数的图象和性质。
点评:典型题,本题将正弦函数与二次函数综合在一起进行考查,对考查学生灵活运用数学知识的能力起到了较好的作用。(2)根据三角函数值范围,确定角的范围易错,应注意结合图象或单位圆加以思考。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.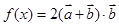
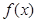 的增区间;
的增区间;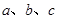 ,若
,若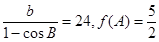 ,求边长
,求边长
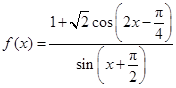 .
.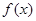 的定义域;
的定义域;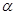 在第一象限且
在第一象限且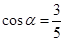 ,求
,求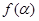 .
. cos2x+sinxcosx
cos2x+sinxcosx .
. ,求函数f(x)的取值范围;
,求函数f(x)的取值范围;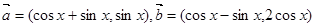 ,设
,设 .
. 的最小正周期,并写出
的最小正周期,并写出 时,求函数
时,求函数 的最小正周期和最小值;
的最小正周期和最小值; 上的单调递增区间.
上的单调递增区间.  的值;
的值; cosx (xÎR).
cosx (xÎR). )=
)= ,求cos2A的值.
,求cos2A的值. 的图象过点
的图象过点 ,且图象上与点P最近的一个最低点是
,且图象上与点P最近的一个最低点是 .
.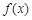 的解析式;
的解析式; ,且
,且 为第三象限的角,求
为第三象限的角,求 的值;
的值; 在区间
在区间 上有零点,求
上有零点,求 的取值范围.
的取值范围.