题目内容
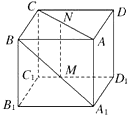
【题目】如图，在小正方形边长为1的网格中画出了某多面体的三视图，则该多面体的外接球表面积为 ． 
【答案】34π
【解析】解：由三视图知，该几何体是三棱锥S﹣ABC，且三棱锥的一个侧面SAC与底面ABC垂直， 其直观图如图所示；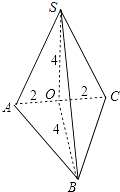
由三视图的数据可得OA=OC=2，OB=OS=4，
建立空间直角坐标系O﹣xyz，如图所示；
则A（0，﹣2，0），B（4，0，0），C（0，2，0），S（0，0，4），
则三棱锥外接球的球心I在平面xOz上，设I（x，0，z）；
由 
得， 
，
解得x=z= 
；
∴外接球的半径R=|BI|= 
= 
，
∴该三棱锥外接球的表面积S=4πR2=4π× 
=34π．
所以答案是：34π．
【考点精析】本题主要考查了简单空间图形的三视图的相关知识点，需要掌握画三视图的原则：长对齐、高对齐、宽相等才能正确解答此题．
练习册系列答案
计算高手系列答案
相关题目
【题目】某公司准备将1000万元资金投入到市环保工程建设中，现有甲、乙两个建设项目选择，若投资甲项目一年后可获得的利润ξ1（万元）的概率分布列如表所示：
ξ1 | 110 | 120 | 170 |
P | m | 0.4 | n |
且ξ1的期望E（ξ1）=120；若投资乙项目一年后可获得的利润ξ2（万元）与该项目建设材料的成本有关，在生产的过程中，公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整，两次调整相互独立且调整的概率分别为p（0＜p＜1）和1﹣p．若乙项目产品价格一年内调整次数X（次数）与ξ2的关系如表所示：
X | 0 | 1 | 2 |
ξ2 | 41.2 | 117.6 | 204.0 |
（Ⅰ）求m，n的值；
（Ⅱ）求ξ2的分布列；
（Ⅲ）若该公司投资乙项目一年后能获得较多的利润，求p的取值范围．
