题目内容
【题目】如图,在四棱锥E﹣ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD.
(Ⅰ)求证:BE=DE;
(Ⅱ)若AB=2 ![]() ,AE=3
,AE=3 ![]() ,平面EBD⊥平面ABCD,直线AE与平面ABD所成的角为45°,求二面角B﹣AE﹣D的余弦值.
,平面EBD⊥平面ABCD,直线AE与平面ABD所成的角为45°,求二面角B﹣AE﹣D的余弦值.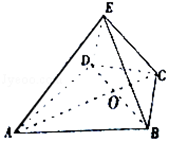
【答案】证明:(Ⅰ)取BD中点O,连结CO,EO, ∵△BCD是等腰三角形,∠BCD=120°,∴CB=CD,∴CO⊥BD,
又∵EC⊥BD,EC∩CO=C,∴BD⊥平面EOC,∴EO⊥BD,
在△BDE中,∵O为BD的中点,∴BE=DE.
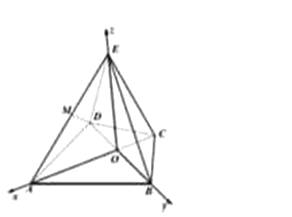
(Ⅱ)∵平面EBD⊥平面ABCD,平面EBD∩平面ABCD=BD,
EO⊥BD,
∴EO⊥平面ABCD,又∵CO⊥BD,AO⊥BD,
∴A,O,C三点共线,AC⊥BD,
以O为原点,OA为x轴,OB为y轴,OE为z轴,建立空间直角坐标系,
在正△ABCD中,AB=2 ![]() ,∴AO=3,BO=DO=
,∴AO=3,BO=DO= ![]() ,
,
∵直线AE与平面ABD所成角为45°,∴EO=AO=3,
A(3,0,0),B(0, ![]() ,0),D(0,﹣
,0),D(0,﹣ ![]() ,0),E(0,0,3),
,0),E(0,0,3),![]() =(﹣3,
=(﹣3, ![]() ,0),
,0), ![]() =(﹣3,﹣
=(﹣3,﹣ ![]() ,0),
,0), ![]() =(﹣3,0,3),
=(﹣3,0,3),
设平面ABE的法向量 ![]() =(a,b,c),
=(a,b,c),
则  ,取a=1,得
,取a=1,得 ![]() =(1,
=(1, ![]() ,1),
,1),
设平面ADE的法向量 ![]() =(x,y,z),
=(x,y,z),
则  ,取x=1,得
,取x=1,得 ![]() =(1,﹣
=(1,﹣ ![]() ,1),
,1),
设二面角B﹣AE﹣D为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
∴二面角B﹣AE﹣D的余弦值为 ![]() .
.
【解析】(Ⅰ)取BD中点O,连结CO,EO,推导出CO⊥BD,EO⊥BD,由此能证明BE=DE.(Ⅱ)以O为原点,OA为x轴,OB为y轴,OE为z轴,建立空间直角坐标系,利用向量法能求出二面角B﹣AE﹣D的余弦值.
【考点精析】通过灵活运用棱锥的结构特征,掌握侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校的学生记者团由理科组和文科组构成,具体数据如下表所示:
组别 | 理科 | 文科 | ||
性别 | 男生 | 女生 | 男生 | 女生 |
人数 | 4 | 4 | 3 | 1 |
学校准备从中选出4人到社区举行的大型公益活动进行采访,每选出一名男生,给其所在小组记1分,每选出一名女生则给其所在小组记2分,若要求被选出的4人中理科组、文科组的学生都有.
(Ⅰ)求理科组恰好记4分的概率?
(Ⅱ)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.

