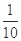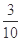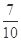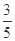题目内容
连续抛掷两颗骰子,点数(x,y)在圆x2+y2=20外的概率为_______.

试题分析:连续抛掷两次骰子分别得到的点数m,n作为点P的坐标所得P点有:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6).共36个。
其中落在圆x2+y2=20外,即满足
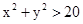 的有:
的有:(1,5),(1,6),(2,5),(2,6),(3,4),(3,5),(3,6),(4,3),(4,4),
(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),
(6,2),(6,3),(6,4),(6,5),(6,6).共23个
故点P落在圆x2+y2=10内(含边界)的概率P=
 。
。点评:中档题,古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解。

练习册系列答案
相关题目
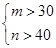 ”的事件A的概率.
”的事件A的概率.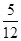
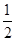
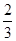
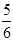
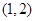 内随机取个实数
内随机取个实数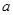 ,则直线
,则直线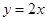 ,直线
,直线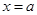 与
与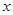 轴围成的面积大于
轴围成的面积大于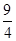 的概率是( )
的概率是( )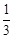
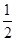
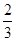
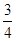
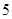 个红球,
个红球,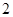 个白球和
个白球和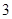 个黑球,乙罐中有
个黑球,乙罐中有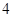 个红球,
个红球,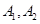 和
和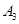 表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以
表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以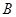 表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。
表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。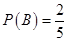 ; ② 事件
; ② 事件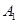 相互独立; ③
相互独立; ③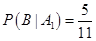
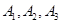 是两两互斥的事件;
是两两互斥的事件; 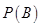 的值不能确定,因为它与
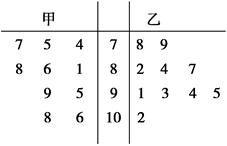
的值不能确定,因为它与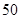 名职工休年假的次数进行的调查统计结果如下表所示:
名职工休年假的次数进行的调查统计结果如下表所示:
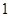
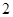
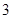
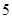

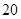
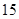
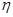 表示这两人休年假次数之和,记“函数
表示这两人休年假次数之和,记“函数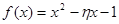 ,在区间
,在区间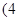 ,
,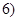 上有且只有一个零点”为事件
上有且只有一个零点”为事件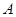 ,求事件
,求事件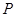 ;
;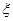 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量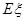 .
.