题目内容
甲同学参加一次英语口语考试,已知在备选的10道题中,甲能答对其中的5道题,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2道题才算合格。则甲合格的概率为
A.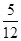 | B.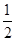 | C.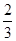 | D.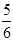 |
B
试题分析:甲要合格,则可以是答对2道或者3道,数目为
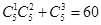 ,总的数目为
,总的数目为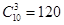 。故选B。
。故选B。点评:求古典概型的概率,只要计算出所求事件的数目和总的数目,然后求出两者的比例即可。

练习册系列答案
相关题目
题目内容
A.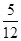 | B.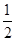 | C.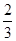 | D.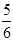 |
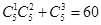 ,总的数目为
,总的数目为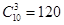 。故选B。
。故选B。