题目内容
在 中,角
中,角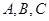 所对的边为
所对的边为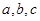 ,已知
,已知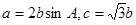
(1)求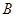 的值;
的值;
(2)若 的面积为
的面积为 ,求
,求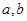 的值
的值
(1)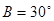
(2) 或
或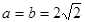
解析试题分析:(Ⅰ)把已知的等式左边利用正弦定理,化边为角,即可求出sinB的值,进而求出B的度数;
(Ⅱ)利用三角形的面积公式表示出△ABC的面积,结合余弦定理和把c,sinB的值代入即可求出c的值,然后由a,c及cosB的值,利用余弦定理即可求出a,b的值
解:(1)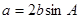 ,
,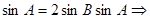
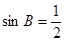 ,
,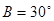 或
或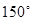 ,
, ,所以
,所以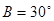 ……………………5分
……………………5分
(2)由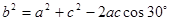
解得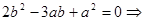
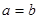 或
或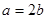 …………① …………8分
…………① …………8分
又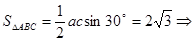
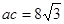 …………②
…………②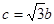 …………③
…………③
由①②③ 或
或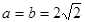 …………12分
…………12分
考点:本题主要考查了学生灵活运用二倍角的正弦、余弦函数公式化简求值,灵活运用同角三角函数间的基本关系及特殊角的三角函数值化简求值,灵活运用三角形的面积公式及余弦定理化简求值,是一道中档题.
点评:解决该试题的关键是边角的转换,是化边为角和,还是化角为边呢,根据表达式合理的选择。

练习册系列答案
相关题目
 中,
中,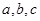 分别是内角
分别是内角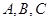 所对的边,且
所对的边,且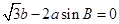 .
. 的大小;
的大小;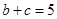 ,且
,且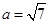 ,求
,求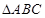 中,
中, 分别为内角
分别为内角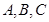 的对边,且
的对边,且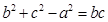 。
。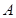 的大小;
的大小;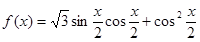 ,求
,求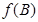 的最大值,并判断此时
的最大值,并判断此时 中,
中, ,
, ,
,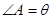 .
. 的表达式
的表达式 、
、 、
、 ,且
,且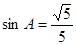 ,
,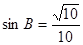 。
。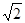 -1,求
-1,求 中,内角
中,内角 所对边的长分别为
所对边的长分别为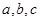 ,已知向量
,已知向量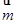 ="(1,cosA" -1),
="(1,cosA" -1),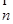 =(cosA,1)且满足
=(cosA,1)且满足 的大小;
的大小; ,求
,求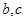 的值.
的值.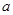 、
、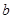 、
、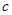 分别是
分别是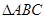 的三个内角
的三个内角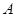 、
、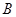 、
、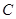 所对的边;
所对的边; ,且
,且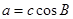 ,且
,且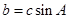 ,试判断
,试判断 、
、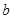 、
、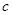 分别是
分别是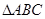 的三个内角
的三个内角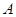 、
、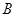 、
、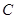 所对的边,(1)若
所对的边,(1)若 求
求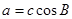 ,且
,且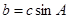 ,试判断
,试判断 ,
,