题目内容
本小题满分10分)
在△ABC中,A、B为锐角,角A、B、C所对的边分别为 、
、 、
、 ,且
,且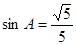 ,
,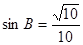 。
。
(1)求角C的值;
(2)若a-b=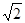 -1,求
-1,求 、
、 、
、 的值。
的值。
(1) ;(2)a=
;(2)a=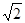 ,b=1,c=
,b=1,c=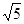 。
。
解析试题分析:∵A、B为锐角,sinA=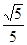 ,sinB=
,sinB= ,
,
∴cosA=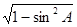 =
=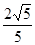 ,cosB=
,cosB=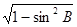 =
=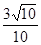 ,
,
∴cosC=-cos(A+B)=-(cosAcosB-sinAsinB)
=-(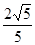 ×
×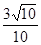 -
-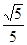 ×
× )=
)= .
.
∵0<C<π,∴C= ---------------5分
---------------5分
(2)由(1)知C=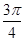 ,∴sinC=
,∴sinC= .
.
由正弦定理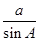 =
=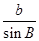 =
=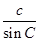 得
得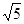 a=
a=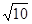 b=
b=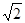 c,即a=
c,即a=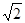 b,c=
b,c=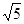 b,
b,
∵a-b=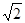 -1,∴
-1,∴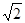 b-b=
b-b=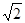 -1,∴b=1,
-1,∴b=1,
∴a=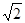 ,c=
,c=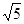 . ---------------10分
. ---------------10分
考点:本题考查正弦定理;诱导公式;三角形内的隐含条件。
点评:熟练掌握公式及定理是解本题的关键.在解题过程中,要仔细计算,避免出现计算错误。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
,
 ,且
,且 ∥
∥ ,
, ,且△ABC的面积小于
,且△ABC的面积小于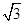 ,求角B的取值范围.
,求角B的取值范围.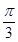 )+sin2x.
)+sin2x.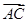 ·
·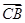 =
=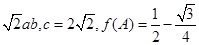 , 求△ABC的面积S.
, 求△ABC的面积S.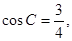
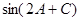 的值。
的值。 中,内角
中,内角 的对边分别为
的对边分别为 。已知
。已知 ,
,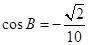 。(1)求
。(1)求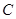 ;(2)若
;(2)若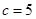 ,求△
,求△ 中,角
中,角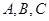 所对的边为
所对的边为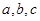 ,已知
,已知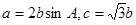
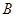 的值;
的值; ,求
,求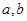 的值
的值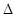 ABC中,BC=
ABC中,BC=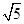 ,AC=3,sinC="2sinA"
,AC=3,sinC="2sinA" 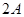 的值.
的值. 的周长为
的周长为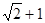 ,且
,且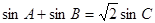
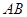 的长;
的长;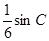 ,求角C的度数.
,求角C的度数.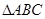 中,内角
中,内角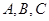 对边的边长分别是
对边的边长分别是 ,已知
,已知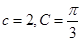 ,
,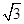 ,求
,求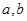 ;
;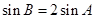 ,求
,求