题目内容
(本题满分12分)已知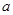 、
、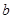 、
、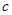 分别是
分别是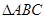 的三个内角
的三个内角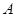 、
、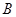 、
、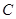 所对的边;
所对的边;
(1)若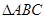 面积
面积 ,且
,且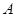 、
、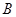 、
、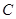 成等差数列,求
成等差数列,求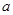 、
、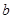 的值;
的值;
(2)若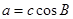 ,且
,且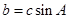 ,试判断
,试判断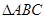 的形状。
的形状。
(1)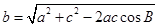 =
=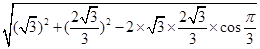 =
=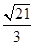 ;
;
(2)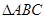 是等腰直角三角形。
是等腰直角三角形。
解析试题分析:①利用△ABC面积为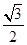 ,c和内角和定理直接求出B,通过余弦定理求出a的值.
,c和内角和定理直接求出B,通过余弦定理求出a的值.
②利用正弦定理化简关系式,求出角的关系即可判断△ABC的形状.
解:(1)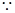
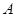 、
、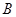 、
、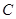 成等差数列,
成等差数列,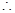
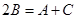 ,…………1分
,…………1分
又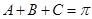
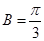 …………2分
…………2分

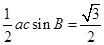 解得
解得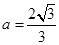 …………4分
…………4分
由余弦定理知,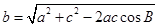
= =
=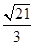 ………6分
………6分
(2)根据余弦定理,由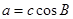 ,得
,得 ,
, 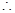
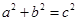 ,
,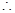
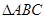 是直角三角形,
是直角三角形, …………10分
…………10分
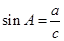 ,
,
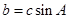 =
= ,
,
故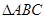 是等腰直角三角形。…………12分
是等腰直角三角形。…………12分
另法:根据正弦定理,由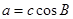 ,得
,得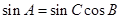 ,又
,又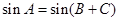
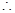

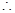
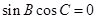
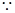
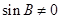 ,
,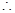
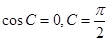 …………10分
…………10分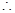
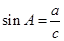 ,
,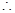
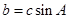 =
= , 故
, 故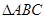 是等腰直角三角形。…………12分
是等腰直角三角形。…………12分
考点:本试题主要考查了正弦定理、余弦定理、三角形的面积公式的应用,考查计算能力
点评:解决该试题的关键是能将已知中等差数列得到角B的值,进而结合面积公式求解a,b的值。

练习册系列答案
相关题目
 的内角A、B、C的对边分别为
的内角A、B、C的对边分别为 ,
,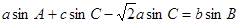
 ,
,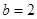 ,求
,求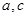
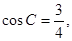
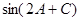 的值。
的值。 中,角
中,角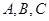 所对的边为
所对的边为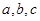 ,已知
,已知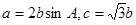
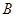 的值;
的值; ,求
,求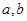 的值
的值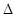 ABC中,BC=
ABC中,BC=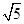 ,AC=3,sinC="2sinA"
,AC=3,sinC="2sinA" 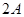 的值.
的值.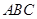 的内角
的内角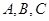 的对边分别为
的对边分别为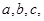
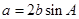
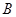 的大小;
的大小;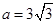 ,
,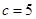 ,求
,求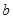 .
. 的周长为
的周长为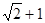 ,且
,且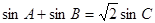
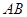 的长;
的长;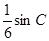 ,求角C的度数.
,求角C的度数. 中,
中,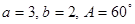 ,求
,求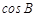 及
及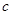 的值.
的值. 中,设角
中,设角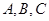 的对边分别是
的对边分别是 ,
,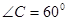 ,
,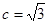 .
.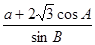 的值;
的值;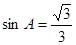 ,求
,求