题目内容
在直角坐标系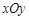 中,点
中,点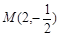 ,点
,点 为抛物线
为抛物线 的焦点,
的焦点,
线段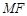 恰被抛物线
恰被抛物线 平分.
平分.
(Ⅰ)求 的值;
的值;
(Ⅱ)过点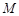 作直线
作直线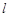 交抛物线
交抛物线 于
于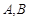 两点,设直线
两点,设直线 、
、 、
、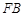 的斜率分别为
的斜率分别为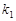 、
、 、
、 ,问
,问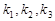 能否成公差不为零的等差数列?若能,求直线
能否成公差不为零的等差数列?若能,求直线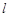 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
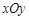 中,点
中,点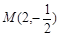 ,点
,点 为抛物线
为抛物线 的焦点,
的焦点,线段
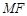 恰被抛物线
恰被抛物线 平分.
平分.(Ⅰ)求
 的值;
的值;(Ⅱ)过点
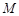 作直线
作直线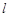 交抛物线
交抛物线 于
于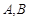 两点,设直线
两点,设直线 、
、 、
、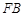 的斜率分别为
的斜率分别为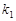 、
、 、
、 ,问
,问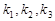 能否成公差不为零的等差数列?若能,求直线
能否成公差不为零的等差数列?若能,求直线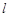 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.(Ⅰ)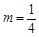 (Ⅱ)
(Ⅱ)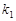 ,
, ,
, 能成公差不为零的等差数列,直线
能成公差不为零的等差数列,直线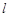 的方程为:
的方程为: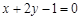
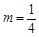 (Ⅱ)
(Ⅱ)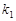 ,
, ,
, 能成公差不为零的等差数列,直线
能成公差不为零的等差数列,直线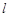 的方程为:
的方程为: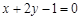
试题分析:(Ⅰ)焦点
 的坐标为
的坐标为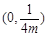 ,线段
,线段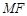 的中点
的中点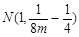 在抛物线
在抛物线 上,
上,∴
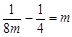 ,
,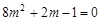 ,∴
,∴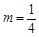 (
(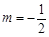 舍) . ……3分
舍) . ……3分(Ⅱ)由(Ⅰ)知:抛物线
 :
: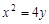 ,
,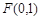 .
.设
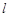 方程为:
方程为: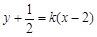 ,
,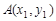 、
、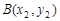 ,则
,则由
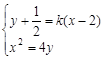 得:
得: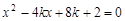 ,
,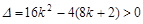 ,∴
,∴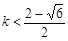 或
或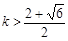 .
.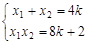 , ……5分
, ……5分假设
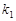 ,
, ,
, 能成公差不为零的等差数列,则
能成公差不为零的等差数列,则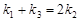 .
.而
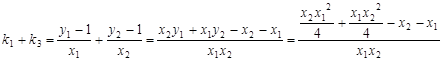
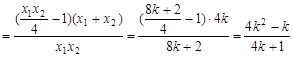 , ……7分
, ……7分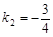 ,∴
,∴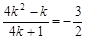 ,
,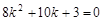 ,解得:
,解得: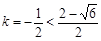 (符合题意),
(符合题意),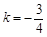 (此时直线
(此时直线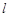 经过焦点
经过焦点 ,
,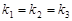 ,不合题意,舍去),
,不合题意,舍去),直线
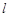 的方程为
的方程为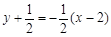 ,即
,即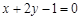 .
. 故
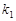 ,
, ,
, 能成公差不为零的等差数列,直线
能成公差不为零的等差数列,直线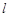 的方程为:
的方程为: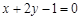 . ……10分
. ……10分点评:解决直线与圆锥曲线的位置,一般免不了联立直线方程和圆锥曲线方程,此时运算量比较大,要仔细运算,而且联立之后,不要忘记验证判别式大于零.

练习册系列答案
相关题目

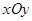 中的抛物线
中的抛物线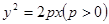 的焦点
的焦点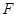 作一条倾斜角为
作一条倾斜角为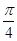 的直线与抛物线相交于A,B两点. 用
的直线与抛物线相交于A,B两点. 用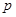 表示A,B之间的距离;
表示A,B之间的距离;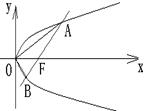
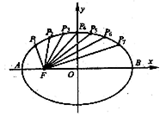
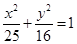 的长轴
的长轴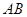 分成
分成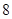 等份,过每个分点作
等份,过每个分点作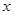 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于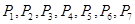 七个点,
七个点,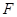 是椭圆的一个焦点则
是椭圆的一个焦点则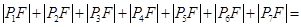 ________________
________________
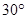 角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
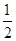
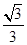
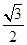
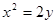 上任意一点
上任意一点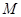 向圆
向圆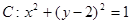 作切线
作切线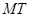 ,则切线长
,则切线长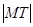 的最小值为
的最小值为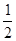
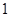
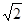
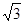
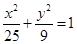 ,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点。设
,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点。设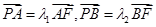 ,则
,则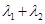 等于( )
等于( )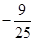 B.
B. 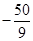 C.
C.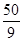 D.
D. 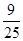
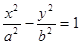 的左、右焦点.若双曲线上存在点A,使
的左、右焦点.若双曲线上存在点A,使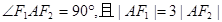 ,则双曲线的离心率为( )
,则双曲线的离心率为( )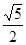
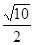

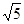
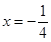

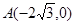 是其左顶点,点C在椭圆上且
是其左顶点,点C在椭圆上且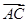 ·
·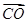 ="0," |
="0," |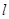 和椭圆交于M,N两个不同点,求
和椭圆交于M,N两个不同点,求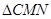 面积的最大值,并求此时直线
面积的最大值,并求此时直线