题目内容
已知等差数列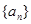 的公差
的公差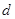 大于0,且
大于0,且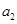 、
、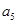 是方程
是方程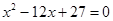 的两根.数列
的两根.数列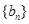 的前
的前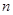 项和为
项和为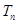 ,满足
,满足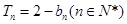
(Ⅰ)求数列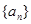 ,
,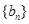 的通项公式;
的通项公式;
(Ⅱ)设数列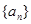 的前
的前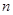 项和为
项和为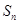 ,记
,记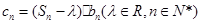 .若
.若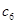 为数列
为数列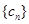 中的最大项,求实数
中的最大项,求实数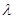 的取值范围.
的取值范围.
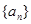 的公差
的公差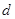 大于0,且
大于0,且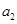 、
、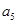 是方程
是方程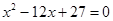 的两根.数列
的两根.数列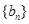 的前
的前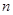 项和为
项和为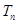 ,满足
,满足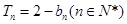
(Ⅰ)求数列
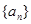 ,
,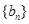 的通项公式;
的通项公式;(Ⅱ)设数列
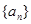 的前
的前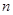 项和为
项和为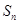 ,记
,记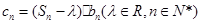 .若
.若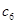 为数列
为数列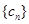 中的最大项,求实数
中的最大项,求实数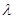 的取值范围.
的取值范围.(1)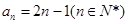 ,
,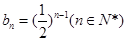 ;(2)
;(2)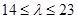 .
.
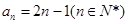 ,
,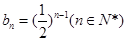 ;(2)
;(2)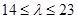 .
. (1)根据韦达定理找出等差数列的项的关系求出公差和首项,再根据定义求出等差数列的通项公式,根据数列前n项和的定义构造递推式,进一步找出数列规律,求出数列的通项;(2)利用条件列出相邻项的不等式,再利用不等式知识求出参数范围
解:(Ⅰ)由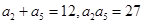 ,且
,且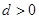 ,所以
,所以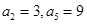 ,
,
从而 ∴
∴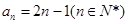 (3分)
(3分)
在已知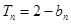 中,令
中,令 ,得
,得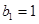
当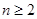 时,
时,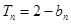 ,
,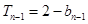 ,两式相减得,
,两式相减得,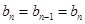 ,
,
∴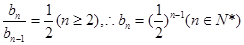 (6分)
(6分)
(Ⅱ)∵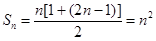
则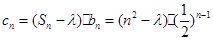 (8分)
(8分)
当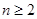 时,
时,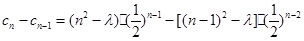
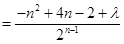
有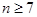 时,
时,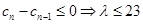
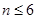 时,
时,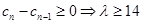
则有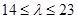 (12分)
(12分)
解:(Ⅰ)由
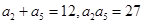 ,且
,且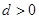 ,所以
,所以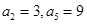 ,
,从而
 ∴
∴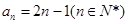 (3分)
(3分)在已知
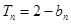 中,令
中,令 ,得
,得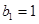
当
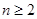 时,
时,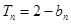 ,
,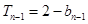 ,两式相减得,
,两式相减得,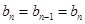 ,
,∴
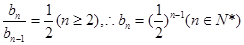 (6分)
(6分)(Ⅱ)∵
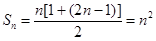
则
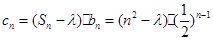 (8分)
(8分)当
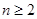 时,
时,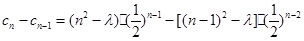
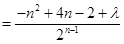
有
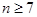 时,
时,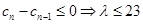
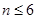 时,
时,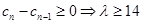
则有
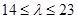 (12分)
(12分)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

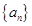 满足
满足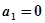 且
且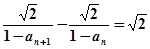 。
。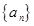 的通项公式;
的通项公式;
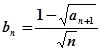 ,记
,记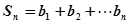 ,证明
,证明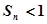 .
.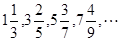 的一个通项公式为
的一个通项公式为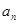 =_______
=_______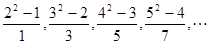 ,则此数列的通项公式
,则此数列的通项公式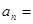 _____;
_____;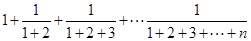 =__________
=__________ 的通项公式为
的通项公式为 ,则此数列的前
,则此数列的前 项的和等于 ( )
项的和等于 ( )



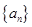 中,
中,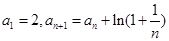 ,则
,则