Question

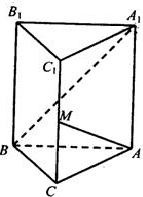如图，在直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，∠BAC=30°，BC=1，AA1=

6

，M是棱CC₁的中点，
（1）求证：A₁B⊥AM；
（2）求直线AM与平面AA₁B₁B所成角的正弦值．

Answer 1

分析：（1）由题意利用几何体的垂直关系建立直角坐标系，求对应向量的数量积为零，即得出垂直；
（2）在（1）的坐标系中，求出面AA₁B₁B的法向量，再利用对应向量的数量积求余弦值的绝对值，即为所求．

解答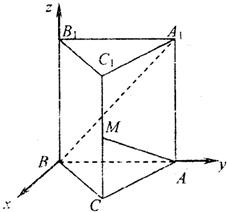：解：（1）如图，以B为原点，BA、BB₁所在直线为y轴、z轴建立空间直角坐标系，
则B（0，0，0），A₁（0，2，

6

），A（0，2，0），M(

3

2

，

1

2

，

6

2

)，
∴

A1B

=(0，-2，-

6

)，

AM

=(

3

2

，-

3

2

，

6

2

)，
∴

A1B

•

AM

=0+3-3=0，
即

A1B

⊥

AM

，∴

A1B

⊥

AM

；
（2）∵x轴⊥面AA₁B₁B，∴面AA₁B₁B的法向量取n=（1，0，0），
设直线AM与平面AA₁B₁B所成角为θ，
∴sinθ=|cos＜

AM

，n＞|=|

AM •n

| AM |•|n|

|=

6

6

，
∴直线AM与平面AA₁B₁B所成角的正弦值为

6

6

．

点评：本题考查了线线垂直和线面角，利用几何体垂直关系建立坐标系，再利用对应向量的数量积证明线线垂直和求解线面角的正弦值，这是立体几何中常用的一种方法．