题目内容
【题目】已知 
≤a≤1，若函数f（x）=ax2﹣2x+1在区间[1，3]上的最大值为M（a），最小值为N（a），令g（a）=M（a）﹣N（a）．
（1）求g（a）的函数表达式；
（2）判断函数g（a）在区间[ ，1]上的单调性，并求出g（a）的最小值．
【答案】
（1）解：f（x）=ax2﹣2x+1的对称轴为x= 
，
∵ 
≤a≤1，∴1≤ ≤3，
∴f（x）在[1，3]上的最小值f（x）min=N（a）=f（ ）=1﹣ ．
∵f（x）=ax2﹣2x+1在区间[1，3]上的最大值为M（a），最小值为N（a），
∴①当1≤ ≤2，即 
≤a≤1时，
M（a）=f（3）=9a﹣5，N（a）=f（ ）=1﹣ ．
g（a）=M（a）﹣N（a）=9a+ ﹣6．
②当2＜ ≤3时．即 ≤a＜ 时，
M（a）=f（1）=a﹣1，N（a）=f（ ）=1﹣ ．
g（a）=M（a）﹣N（a）=a+ ﹣2．
∴g（a）=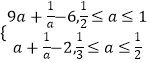 
（2）解：由（1）可知当 ≤a≤1时，g（a）=M（a）﹣N（a）=9a+ ﹣6≥0，当且仅当a= 时取等号，所以它在[ ，1]上单调递增；
当 ≤a＜ 时，g（a）=M（a）﹣N（a）=a+ ﹣2≥0，当且仅当a=1时取等号，所以g（a）在[ 
]单调递减．
∴g（a）的最小值为g（ ）=9× 
【解析】（1）明确f（x）=ax2﹣2x+1的对称轴为x= ，由 ≤a≤1，知1≤ ≤3，可知f（x）在[1，3]上单调递减，N（a）=f（ ）=1﹣ ．由a的符号进行分类讨论，能求出g（a）的解析式；（2）根据（1）的解答求g（a）的最值．
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识，掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较，以及对二次函数在闭区间上的最值的理解，了解当
时，当
时，
；当
时在
上递减，当时，
．
