题目内容
(14分)若数列![]() 满足
满足![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 为等方差数列.已知等方差数列
为等方差数列.已知等方差数列![]() 满足
满足![]()
![]() 成等比数列且互不相等.
成等比数列且互不相等.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和;
项和;
解析:(Ⅰ)由![]() 得,
得,![]()
即 ![]()
![]()
![]() ,
,
![]()
数列![]() 的通项公式为
的通项公式为![]() ; …………………………………5分
; …………………………………5分
![]() (Ⅱ)
(Ⅱ) ![]()
设 ![]() ①
①
![]() ②
②
①-②,得
![]()
![]()

![]()
![]() .
.
即数列![]() 的前
的前![]() 项和为
项和为![]() ;…………………………………10分
;…………………………………10分
(Ⅲ)假设存在实数![]() ,使得对一切正整数
,使得对一切正整数![]() ,总有
,总有![]() 成立,
成立,
即 ![]() .
.
设 ![]()
![]() ,
,
当 ![]() 时,
时,![]() ,且
,且![]() 递减;当
递减;当 ![]() 时,
时,![]() ,且
,且![]() 递减;故
递减;故
![]() 最大,
最大, ![]()
![]() .
.
![]()
故存在![]() ,使得对一切正整数
,使得对一切正整数![]() ,总有
,总有![]() 成立.
成立.
……………………………………14分

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
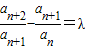 (λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 .
(λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 . ,则数列{an}是比等差数列,且比公差λ=2;
,则数列{an}是比等差数列,且比公差λ=2; ,a1=2,则此数列的通项为
,a1=2,则此数列的通项为 -1,且{an}不是比等差数列;
-1,且{an}不是比等差数列; ,且an=
,且an= ,则此数列的通项为an=
,则此数列的通项为an= ,且{an}不是比等差数列.
,且{an}不是比等差数列. (λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 .
(λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 . ,则数列{an}是比等差数列,且比公差λ=2;
,则数列{an}是比等差数列,且比公差λ=2; ,a1=2,则此数列的通项为
,a1=2,则此数列的通项为 -1,且{an}不是比等差数列;
-1,且{an}不是比等差数列; ,且an=
,且an= ,则此数列的通项为an=
,则此数列的通项为an= ,且{an}不是比等差数列.
,且{an}不是比等差数列.