题目内容
在数列{an}中,如果对任意的n∈N*,都有 (λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 .
(λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 .①若数列{Fn}满足F1=1,F2=1,Fn=Fn-1+Fn-2(n≥3),则该数列不是比等差数列;
②若数列{an}满足
 ,则数列{an}是比等差数列,且比公差λ=2;
,则数列{an}是比等差数列,且比公差λ=2;③等差数列是常数列是成为比等差数列的充分必要条件;
(文)④数列{an}满足:
 ,a1=2,则此数列的通项为
,a1=2,则此数列的通项为 -1,且{an}不是比等差数列;
-1,且{an}不是比等差数列;(理)④数列{an}满足:a1=
 ,且an=
,且an= ,则此数列的通项为an=
,则此数列的通项为an= ,且{an}不是比等差数列.
,且{an}不是比等差数列.
【答案】分析:根据比等差数列的定义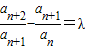 (λ为常数),逐一判断①~④中的四个数列是否是比等差数列,即可得到答案.
(λ为常数),逐一判断①~④中的四个数列是否是比等差数列,即可得到答案.
解答:解:数列{Fn}满足F1=1,F2=1,F3=2,F4=3,F5=5,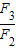 -
-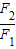 =1,
=1,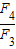 -
-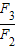 =-
=- ≠1,
≠1,
则该数列不是比等差数列,
故①正确;
若数列{an}满足an=(n-1)•2n-1,
则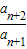 -
-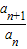 =
=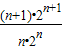 -
-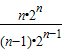 =
=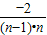 不为定值,
不为定值,
即数列{an}不是比等差数列,
故②错误;
③当等差数列为常数列0,0,0,0,…,0时,不能成为比等差数列,
故③错误;
(文)④∵数列{an}满足: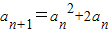 ,
,
a1=2= -1,
-1,
∴a2=4+4=8=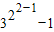 ,
,
a3=64+16=80=3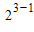 -1.
-1.
由此猜想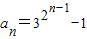 .
.
用数学归纳法证明:
①当n=1时,a1=2= -1,成立.
-1,成立.
②假设当n=k时成立,即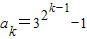 ,
,
则ak+1=(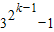 )2+2(
)2+2(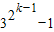 )
)
=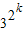 -2×3
-2×3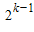 +1-2×
+1-2×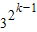 -2
-2
=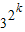 -1,也成立,
-1,也成立,
∴此数列的通项为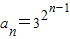 -1.
-1.
∴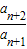 -
-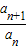 =
=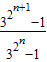 -
-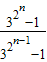 不是常数,
不是常数,
故{an}不是比等差数列,故④正确;
(理)④∵数列{an}满足:a1= ,且an=
,且an=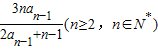 ,
,
∴a1= =
=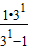 ,
,
a2=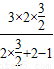 =
= =
=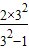 ,
,
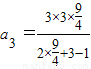 =
=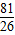 =
=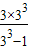 .
.
由此猜想an=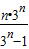 .
.
用数学归纳法证明:
①当n=1时,a1= =
=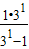 ,成立;
,成立;
②假设n=k时,等式成立,即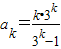 ,
,
则ak+1=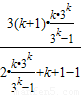 =
=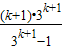 ,也成立.
,也成立.
故此数列的通项为an= ,
,
∴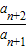 -
-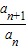 =
=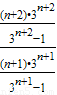 -
-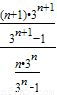 不是常数,
不是常数,
故{an}不是比等差数列,故④正确;
故答案为:①④.
点评:本题考查新定义,解题时应正确理解新定义,同时注意利用列举法判断命题为假,属于难题.
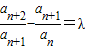 (λ为常数),逐一判断①~④中的四个数列是否是比等差数列,即可得到答案.
(λ为常数),逐一判断①~④中的四个数列是否是比等差数列,即可得到答案.解答:解:数列{Fn}满足F1=1,F2=1,F3=2,F4=3,F5=5,
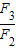 -
-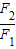 =1,
=1,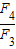 -
-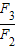 =-
=- ≠1,
≠1,则该数列不是比等差数列,
故①正确;
若数列{an}满足an=(n-1)•2n-1,
则
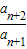 -
-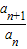 =
=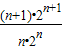 -
-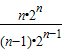 =
=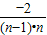 不为定值,
不为定值,即数列{an}不是比等差数列,
故②错误;
③当等差数列为常数列0,0,0,0,…,0时,不能成为比等差数列,
故③错误;
(文)④∵数列{an}满足:
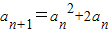 ,
,a1=2=
 -1,
-1,∴a2=4+4=8=
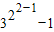 ,
,a3=64+16=80=3
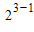 -1.
-1.由此猜想
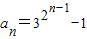 .
.用数学归纳法证明:
①当n=1时,a1=2=
 -1,成立.
-1,成立.②假设当n=k时成立,即
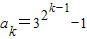 ,
,则ak+1=(
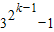 )2+2(
)2+2(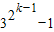 )
)=
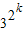 -2×3
-2×3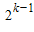 +1-2×
+1-2×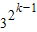 -2
-2=
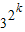 -1,也成立,
-1,也成立,∴此数列的通项为
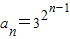 -1.
-1.∴
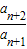 -
-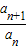 =
=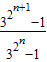 -
-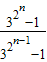 不是常数,
不是常数,故{an}不是比等差数列,故④正确;
(理)④∵数列{an}满足:a1=
 ,且an=
,且an=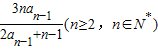 ,
,∴a1=
 =
=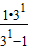 ,
,a2=
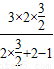 =
= =
=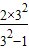 ,
,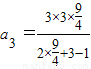 =
=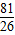 =
=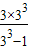 .
.由此猜想an=
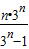 .
.用数学归纳法证明:
①当n=1时,a1=
 =
=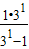 ,成立;
,成立;②假设n=k时,等式成立,即
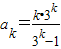 ,
,则ak+1=
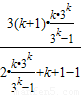 =
=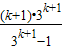 ,也成立.
,也成立.故此数列的通项为an=
 ,
,∴
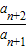 -
-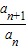 =
=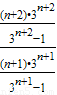 -
-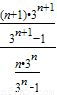 不是常数,
不是常数,故{an}不是比等差数列,故④正确;
故答案为:①④.
点评:本题考查新定义,解题时应正确理解新定义,同时注意利用列举法判断命题为假,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 6、在数列{an}中,a1=1,an=an-1+n,n≥2.为计算这个数列前10项的和,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是( )
6、在数列{an}中,a1=1,an=an-1+n,n≥2.为计算这个数列前10项的和,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是( ) 在数列{an}中,a1=1,an=an-1+n,n≥2.为计算这个数列前5项的和,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处应填
在数列{an}中,a1=1,an=an-1+n,n≥2.为计算这个数列前5项的和,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处应填