题目内容
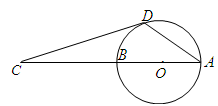
如图,已知在△ABC中,AB=AC,D是△ABC外接圆劣弧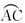 上的点(不与点A,C重合),延长BD至E.
上的点(不与点A,C重合),延长BD至E.
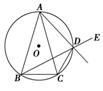
(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30°,△ABC中BC边上的高为2+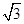 ,求△ABC外接圆的面积.
,求△ABC外接圆的面积.
 上的点(不与点A,C重合),延长BD至E.
上的点(不与点A,C重合),延长BD至E.
(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30°,△ABC中BC边上的高为2+
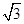 ,求△ABC外接圆的面积.
,求△ABC外接圆的面积.(1)见解析(2)见解析
如图,设F为AD延长线上一点.
∵A、B、C、D四点共圆,
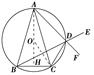
∴∠CDF=∠ABC.又AB=AC,∴∠ABC=∠ACB,且∠ADB=∠ACB,
∴∠ADB=∠CDF.又∠EDF=∠ADB,
故∠EDF=∠CDF,即AD的延长线平分∠CDE.
(2)设O为外接圆圆心,连接AO交BC于H,则AH⊥BC.
连接OC,由题意∠OAC=∠OCA=15°,∠ACB=75°,∴∠OCH=60°.
设圆半径为r,则r+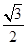 r=2+
r=2+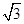 ,得r=2,外接圆面积为4π.
,得r=2,外接圆面积为4π.
∵A、B、C、D四点共圆,

∴∠CDF=∠ABC.又AB=AC,∴∠ABC=∠ACB,且∠ADB=∠ACB,
∴∠ADB=∠CDF.又∠EDF=∠ADB,
故∠EDF=∠CDF,即AD的延长线平分∠CDE.
(2)设O为外接圆圆心,连接AO交BC于H,则AH⊥BC.
连接OC,由题意∠OAC=∠OCA=15°,∠ACB=75°,∴∠OCH=60°.
设圆半径为r,则r+
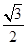 r=2+
r=2+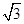 ,得r=2,外接圆面积为4π.
,得r=2,外接圆面积为4π.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
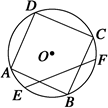
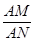 =
=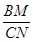 ,下列结论中正确的是 ( ).
,下列结论中正确的是 ( ).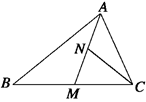
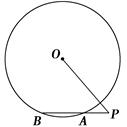
 是
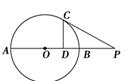
是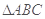 的外接圆,过点C的切线交
的外接圆,过点C的切线交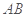 的延长线于点
的延长线于点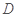 ,
,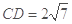 ,
,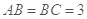 。则
。则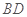 的长___________(2分)AC的长______________(3分).
的长___________(2分)AC的长______________(3分). 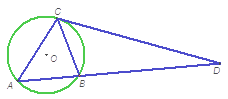
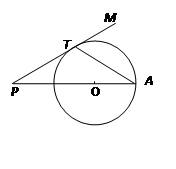
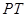 为圆
为圆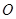 的切线,
的切线,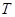 为切点,
为切点,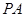 过圆心
过圆心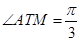 ,圆
,圆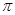 ,则
,则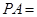 .
.
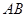 是⊙
是⊙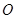 的直径,点
的直径,点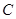 在
在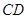 与⊙
与⊙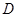 .若
.若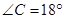 ,则
,则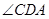 =_____________.
=_____________.