题目内容
【题目】某中学为研究学生的身体素质与体育锻炼时间的关系,对该校200名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面![]() 列联表;
列联表;
锻炼不达标 | 锻炼达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
并通过计算判断,是否能在犯错误的概率不超过0.025的前提下认为“锻炼达标”与性别有关?
(2)在“锻炼达标”的学生中,按男女用分层抽样方法抽出5人,进行体育锻炼体会交流,从参加体会交流的5人中,随机选出2人作重点发言,求恰好选出一名男生的概率.
参考公式: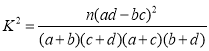 ,其中
,其中![]()
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)![]() 列联表答案见解析,在犯错误的概率不超过0.01的前提下不能判断“课外体育达标”与性别有关;(2)
列联表答案见解析,在犯错误的概率不超过0.01的前提下不能判断“课外体育达标”与性别有关;(2)![]()
【解析】
(1)计算出观测值![]() ,结合临界值表可得结论;
,结合临界值表可得结论;
(2)在“锻炼达标”的学生有50人中,男女生人数比为![]() ,故用分层抽样方法抽取5人,有3人是男生,记为a,b,c,有2人是女生,记为d,e,用列举法以及古典概型概率公式可得结果.
,故用分层抽样方法抽取5人,有3人是男生,记为a,b,c,有2人是女生,记为d,e,用列举法以及古典概型概率公式可得结果.
(1)列出列联表,
课外体育不达标 | 课外体育达标 | 合计 | |
男 | 60 | 30 | 90 |
女 | 90 | 20 | 110 |
合计 | 150 | 50 | 200 |
![]()
所以在犯错误的概率不超过0.01的前提下不能判断“课外体育达标”与性别有关;
(2)“锻炼打标”的学生有50人,男女生人数比为![]() ,故用分层抽样
,故用分层抽样
方法抽取5人,有3人是男生,记为a,b,c,有2人是女生,记为d,e,
则从这5人中选出2人,选法有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,共10种,
,共10种,
设事件A表示 “作重点发言的2人中,恰好有1名男生”,
则事件A包含的基本事件有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6个,
共6个,
![]() .
.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度,某地区在2015年以前的年均脱贫率(脱贫的户数占当年贫困户总数的比)为70%,2015年开始全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加户数占2019年贫困总户数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 |
参加占户比 | 45% | 45% | 10% |
脱贫率 | 96% | 96% | 90% |
那么2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )倍.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()