题目内容
5.用数学归纳法证明:“2n>n2+1对于n>n0的正整数n成立”时,第一步证明中的起始值n0应取5.分析 根据数学归纳法的步骤,结合本题的题意,是要验证n=1,2,3,4,5时,命题是否成立;可得答案.
解答 解:根据数学归纳法的步骤,首先要验证当n取第一个值时命题成立;
结合本题,要验证n=1时,左=21=2,右=12+1=2,2n>n2+1不成立,
n=2时,左=22=4,右=22+1=5,2n>n2+1不成立,
n=3时,左=23=8,右=32+1=10,2n>n2+1不成立,
n=4时,左=24=16,右=42+1=17,2n>n2+1不成立,
n=5时,左=25=32,右=52+1=26,2n>n2+1成立,
因为n>5成立,所以2n>n2+1恒成立.
故答案为:5.
点评 本题考查数学归纳法的运用,解此类问题时,注意n的取值范围.

练习册系列答案
相关题目
10.“φ=$\frac{π}{2}$”是“曲线y=sin(x+φ)关于y轴对称”的( )
| A. | 充要条件 | B. | 充分且不必要条件 | ||
| C. | 必要且不充分条件 | D. | 既不充分也不必要条件 |
17.在平面几何中有“三角形的两边之和大于第三边”;在立体几何中“四面体任意三个面的面积之和( )第四个面的面积”.
| A. | 等于 | B. | 小于 | C. | 大于 | D. | 不能确定 |
 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, ,侧面
,侧面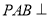 底面
底面 ,
,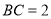 .
.
 平面
平面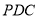 ;
;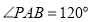 ,求点
,求点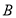 到直线
到直线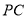 的距离.
的距离. 如图:一个周长为1的圆沿着边长为2的正方形的边按逆时针方向滚动(无滑动),P是圆上的一定点,开始时PA⊥AB,当圆滚过正方形一周,回到起点时,点P所绘出的图形大致是( )
如图:一个周长为1的圆沿着边长为2的正方形的边按逆时针方向滚动(无滑动),P是圆上的一定点,开始时PA⊥AB,当圆滚过正方形一周,回到起点时,点P所绘出的图形大致是( )