题目内容
12.已知函数f(x)=2x,且f(a)=3,函数g(x)=2ax-$\frac{3}{2}$•9x.(1)求常数a的值,并求g(x)的解析式;
(2)当x∈[-2,1]时,求g(x)的值域.
分析 (1)由f(a)=3,化为2a=3,解得a=log23.可得2ax=(2a)x=3x.即可得出g(x).
(2)由x∈[-2,1],可得3x∈$[\frac{1}{9},3]$.g(x)=$-\frac{3}{2}•({3}^{x})^{2}$+3x=$-\frac{3}{2}$$({3}^{x}-\frac{1}{3})^{2}$+$\frac{1}{6}$,再利用二次函数的单调性即可得出.
解答 解:(1)∵f(a)=3,∴2a=3,解得a=log23.
∴2ax=(2a)x=3x.
函数g(x)=2ax-$\frac{3}{2}$•9x=3x-$\frac{3}{2}•{9}^{x}$.
(2)∵x∈[-2,1],∴3x∈$[\frac{1}{9},3]$.
g(x)=$-\frac{3}{2}•({3}^{x})^{2}$+3x=$-\frac{3}{2}$$({3}^{x}-\frac{1}{3})^{2}$+$\frac{1}{6}$,
∴当3x=$\frac{1}{3}$时,g(x)取得最大值$\frac{1}{6}$.
又g(-2)=$\frac{5}{54}$,g(1)=-$\frac{21}{2}$,
∴函数g(x)的最小值为:-$\frac{21}{2}$.
∴g(x)的值域是$[-\frac{21}{2},\frac{1}{6}]$.
点评 本题考查了指数函数与对数函数的单调性、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.偶函数f(x)的定义域为R,且在(-∞,0)上是减函数,且f(-1)=M与f(a2-a+$\frac{5}{4}$)=N(a∈R)的大小( )
| A. | M≤N | B. | M≥N | C. | M<N | D. | M>N |
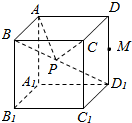 在棱长为1的正方体ABCD-A1B1C1D1中,点P是它的体对角线BD1上一动点,则|AP|+|PC|的最小值是$\frac{2\sqrt{6}}{3}$.
在棱长为1的正方体ABCD-A1B1C1D1中,点P是它的体对角线BD1上一动点,则|AP|+|PC|的最小值是$\frac{2\sqrt{6}}{3}$.