题目内容
4.已知函数y=f(x)与y=g(x)的图象如图所示,则函数y=f(x)•g(x)的图象为( )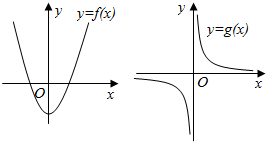
| A. | 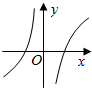 | B. | 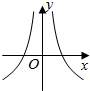 | C. | 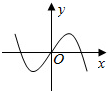 | D. | 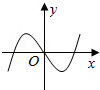 |
分析 本题考查的知识点是函数的图象,由已知中函数y=f(x)与y=g(x)的图象我们不难分析,当函数y=f(x)•g(x)有两个零点M,N,我们可以根据函数y=f(x)与y=g(x)的图象中函数值的符号,分别讨论(-∞,M)(M,0)(0,N)(N,+∞)四个区间上函数值的符号,以确定函数的图象.
解答 解:由题意f(-x)g(-x)=-f(x)g(x),
∴函数y=f(x)•g(x)是奇函数.
∵y=f(x)的有两个零点,并且g(x)没有零点;
∴函数y=f(x)•g(x)也有两个零点M,N,
又∵x=0时,函数值不存在
∴y在x=0的函数值也不存在
当x∈(-∞,M)时,y<0;
当x∈(M,0)时,y>0;
当x∈(0,N)时,y<0;
当x∈(N,+∞)时,y>0;
只有A中的图象符合要求
故选:A.
点评 要根据已知两个函数的图象,判断未知函数的图象,我们关键是要根据已知条件中的函数的图象,分析出未知函数零点的个数,及在每个区间上的符号,然后对答案中的图象逐一进行判断,然后选出符合分析结果的图象.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
16.下列命题正确的是( )
| A. | 方程$\frac{x}{y-2}=1$表示斜率为1,在y轴上的截距是2的直线 | |
| B. | △ABC的顶点坐标分别为A(0,3),B(-2,0),C(2,0),则中线AO的方程是x=0 | |
| C. | 到x轴距离为5的点的轨迹方程是y=5 | |
| D. | 曲线2x2-3y2-2x+m=0通过原点的充要条件是m=0 |