题目内容
高二年级某三个班级参加“深圳市第二高级中学第一届数学竞赛”分别有1,2,3名同学获奖,并站成一排合影留念,若相同班级的同学不能相邻,则有( )种排法.
| A.72 | B.108 | C.120 | D.144 |
设有1名同学获奖班级中的这名同学为A,有2名同学获奖班级中的2名同学为B1、B2,有3名同学获奖班级中的3名同学为C1、C2、C3,
分2步来分析:
①、先排C1、C2、C3,有A33=6种不同的顺序,
②、将A与B1、B2插入其中,分两种情况讨论:
若A与B1、B2中1个排在一起,有2×2×2=8种情况,若A单独插入,则有2×A33=12种情况,
故A与B1、B2有12+8=20种不同的插入方法,
故相同班级的同学不能相邻排法有6×20=120种;
故选C.
分2步来分析:
①、先排C1、C2、C3,有A33=6种不同的顺序,
②、将A与B1、B2插入其中,分两种情况讨论:
若A与B1、B2中1个排在一起,有2×2×2=8种情况,若A单独插入,则有2×A33=12种情况,
故A与B1、B2有12+8=20种不同的插入方法,
故相同班级的同学不能相邻排法有6×20=120种;
故选C.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
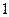 、
、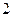 、
、 、
、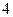 、
、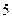 组成没有重复数字的五位数,其中小于
组成没有重复数字的五位数,其中小于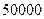 的偶数共有( )
的偶数共有( ) 个
个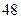 个
个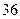 个
个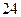 个
个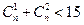 ,则自然数
,则自然数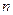 的最大值为( )
的最大值为( )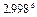 的近似值(精确到小数后第三位)为
的近似值(精确到小数后第三位)为