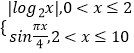题目内容
【题目】【2017辽宁鞍山市最后一次模】如图所示,在三棱锥![]() 中,侧面
中,侧面![]() ,
, ![]() 是全等的直角三角形,
是全等的直角三角形, ![]() 是公共的斜边且
是公共的斜边且![]() ,
, ![]() ,另一侧面
,另一侧面![]() 是正三角形.
是正三角形.

(1)求证: ![]() ;
;
(2)若在线段![]() 上存在一点
上存在一点![]() ,使
,使![]() 与平面
与平面![]() 成
成![]() 角,试求二面角
角,试求二面角![]() 的余弦值.
的余弦值.
【答案】见解析
【解析】(1)证明:作![]() 面
面![]() 于
于![]() ,连接
,连接![]() ,由题意得,
,由题意得, ![]() ,故
,故![]() 中,
中, ![]() ,所以
,所以![]() 为直角三角形,
为直角三角形, ![]() ,又
,又![]() 为
为![]() 在平面
在平面![]() 内的射影,
内的射影, ![]() ,同理得
,同理得![]() ,又
,又![]() ,所以四边形
,所以四边形![]() 是正方形且
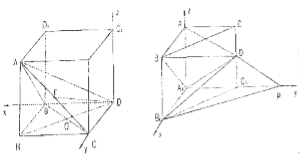
是正方形且![]() ,将所得四棱锥补成正方体,建立如图所示的空间直角坐标系,则
,将所得四棱锥补成正方体,建立如图所示的空间直角坐标系,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() ,则
,则![]() .
.
(2)设![]() 是线段上
是线段上![]() 上一点,则
上一点,则![]() ,
, ![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,
, ![]() ,要使
,要使![]() 与平面
与平面![]() 成
成![]() 角,由图可知,
角,由图可知, ![]() 与
与![]() 的夹角为
的夹角为![]() ,所以
,所以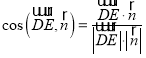
![]() ,则
,则![]() ,解得
,解得![]() ,则
,则![]() ,故线段
,故线段![]() 上存在
上存在![]() 点,当
点,当![]() 时,
时, ![]() 与平面
与平面![]() 成
成![]() 角.
角.
![]()
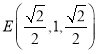 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, 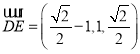 ,设平面
,设平面![]() 的法向量
的法向量![]() ,
,
则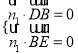 ,
, ![]()
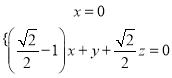 ,令
,令![]() 则
则![]() ,
,
![]()
![]() ,同理平面
,同理平面![]() 的法向量
的法向量![]() ,
,
![]()
![]()
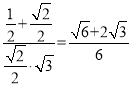 ,设平面
,设平面![]() 与平面
与平面![]() 成角为
成角为![]() ,
,
则![]() .
.

练习册系列答案
相关题目
【题目】从某大学一年级女生中,选取身高分别是150cm、155cm、160cm、165cm、170cm的学生各一名,其身高和体重数据如表所示:
身高/cm(x) | 150 | 155 | 160 | 165 | 170 |
体重/kg(y) | 43 | 46 | 49 | 51 | 56 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,计算身高为168cm时,体重的估计值 ![]() 为多少?
为多少?
参考公式:线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =
=  =
= 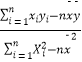 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.