题目内容
若函数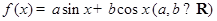 ,非零向量
,非零向量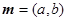 ,我们称
,我们称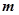 为函数
为函数 的“相伴向量”,
的“相伴向量”, 为向量
为向量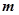 的“相伴函数”.
的“相伴函数”.
(1)已知函数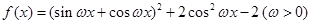 的最小正周期为
的最小正周期为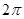 ,求函数
,求函数 的“相伴向量”;
的“相伴向量”;
(2)记向量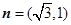 的“相伴函数”为
的“相伴函数”为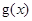 ,将
,将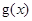 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移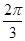 个单位长度,得到函数
个单位长度,得到函数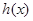 ,若
,若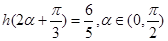 ,求
,求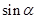 的值;
的值;
(3)对于函数 ,是否存在“相伴向量”?若存在,求出
,是否存在“相伴向量”?若存在,求出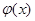 “相伴向量”;
“相伴向量”;
若不存在,请说明理由.
(1)(1,1);(2) ;(3)不存在“相伴向量”
;(3)不存在“相伴向量”
解析试题分析:(1)由函数 平方项展开化简,再通过化一公式即可得一个函数的形式,又因为最小正周期为
平方项展开化简,再通过化一公式即可得一个函数的形式,又因为最小正周期为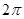 ,即可求得
,即可求得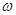 的值.再将函数展开写成
的值.再将函数展开写成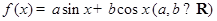 的形式及可得结论.
的形式及可得结论.
(2)由向量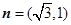 为函数
为函数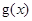 的“相伴向量”,所以可得到函数
的“相伴向量”,所以可得到函数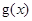 .再将
.再将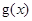 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移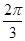 个单位长度,得到函数
个单位长度,得到函数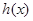 .再根据
.再根据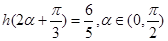 .通过解三角方程即可得到所求的结论.
.通过解三角方程即可得到所求的结论.
(3)对于函数 ,是否存在“相伴向量”.通过反证法的思想,可证明不存在函数
,是否存在“相伴向量”.通过反证法的思想,可证明不存在函数 的“相伴向量”.
的“相伴向量”.
(1)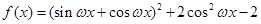
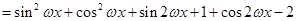
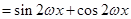
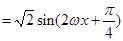 , 1分
, 1分
依题意得 ,故
,故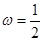 . 2分
. 2分
∴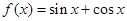 ,即
,即 的“相伴向量”为(1,1). 3分
的“相伴向量”为(1,1). 3分
(2)依题意,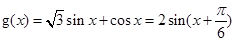 , 4分
, 4分
将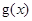 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
得到函数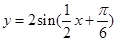 , 5分
, 5分
再将所得的图象上所有点向左平移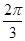 个单位长度,得到
个单位长度,得到 ,
,
即 , 6分
, 6分
∵ ,∴
,∴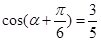 ,
,
∵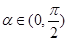 ,∴
,∴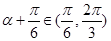 ,∴
,∴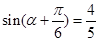 , 8分
, 8分
∴ . 10分
. 10分
(3)若函数 存在“相伴向量”,
存在“相伴向量”,
则存在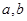 ,使得
,使得 对任意的
对任意的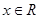 都成立, 11分
都成立, 11分
令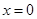 ,得
,得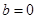 ,
,
因此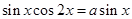 ,即
,即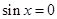 或
或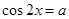 ,
,
显然上式对任意的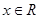 不都成立,
不都成立,
所以函数 不存在“相伴向量”. 13分
不存在“相伴向量”. 13分
(注:本题若化成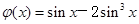 ,直接说明不存在的,给1分)
,直接说明不存在的,给1分)
考点:1.三角函数的性质.2.三角恒等变换.3.三角函数的图象.4.新定义问题.5.反正的思想.

 ,
, .
. 值; (2)求
值; (2)求 的值.
的值.
 时,求
时,求 的值;
的值;  在
在 上的值域.
上的值域.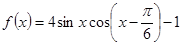
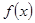 的最小正周期;
的最小正周期;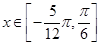 时,求函数
时,求函数 ,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π.
,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π. ,f
,f =
= ,f
,f =-
=- ,求sin(α+β)的值.
,求sin(α+β)的值.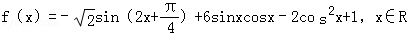 .
.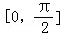 上的最大值和最小值.
上的最大值和最小值.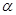 为第四象限角,其终边上的一个点是
为第四象限角,其终边上的一个点是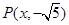 ,且
,且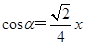 ,求
,求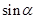 和
和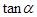 .
.
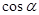 的值;
的值;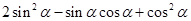 的值.
的值.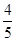 ,求S△AOB.
,求S△AOB.