题目内容
给出下列命题:
①函数 与函数
与函数 的图象关于
的图象关于 对称
对称
②函数 导函数为
导函数为 ,若
,若 ,则
,则 必为函数
必为函数 的极值.
的极值.
③函数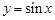 在一象限单调递增
在一象限单调递增
④ 在其定义域内为单调增函数.
在其定义域内为单调增函数.
其中正确的命题序号为
【答案】
①
【解析】
试题分析:对于①函数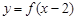 表示的是将y=f(x)右移2个范围得到,而函数
表示的是将y=f(x)右移2个范围得到,而函数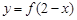 的图象是将f(x)关于y轴对称,再向右移2个单位,因此可知其图像关于
的图象是将f(x)关于y轴对称,再向右移2个单位,因此可知其图像关于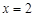 对称,成立。
对称,成立。
对于②函数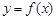 导函数为
导函数为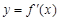 ,若
,若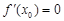 ,则
,则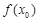 必为函数
必为函数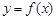 的极值.比如二次函数y=x3,在x=0处不是极值点,但是导数为零的点。故错误。
的极值.比如二次函数y=x3,在x=0处不是极值点,但是导数为零的点。故错误。
对于③函数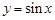 在一象限单调递增,不成立因为角不在一个单调区间内,因为有周期性,错误。
在一象限单调递增,不成立因为角不在一个单调区间内,因为有周期性,错误。
对于④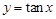 在其定义域内为单调增函数.应该是在每一个区间内递增,不满足单调性定义,错误。故填写①
在其定义域内为单调增函数.应该是在每一个区间内递增,不满足单调性定义,错误。故填写①
考点:本题主要是考查函数图像的变换,以及导数为零点与函数在该点是否取得极值扽问题的运用。
点评:解决该试题的关键是理解单调性和图像的对称性的概念,并能利用条件逐一的加以判定,得到结论。

练习册系列答案
相关题目