题目内容
已知x、y满足不等式组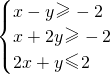 ,若O为坐标原点,M(x,y),N(1,-2),则
,若O为坐标原点,M(x,y),N(1,-2),则 •
• 的最小值是________.
的最小值是________.
-4
分析:由不等式组画出可行域,再由给出的两个点的坐标写出 •
• 的表达式,利用线性规划知识求线性目标函数的最小值.
的表达式,利用线性规划知识求线性目标函数的最小值.
解答:由不等式组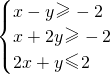 得可行域为△ABC的边界及其内部,如图,
得可行域为△ABC的边界及其内部,如图,

由x-y=-2,2x+y=2解得A(0,2).
由x-y=-2,x+2y=-2解得B(-2,0).
由x+2y=-2,2x+y=2解得C(2,-2).
∵M(x,y),N(1,-2),∴ =(x,y),
=(x,y), =(1,-2).
=(1,-2).
则 •
• =x-2y.
=x-2y.
令z= •
• =x-2y,则
=x-2y,则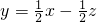 ,
,
要使z最小,则直线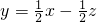 在y轴上的截距最大.
在y轴上的截距最大.
由可行域可知,当直线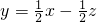 过点A(0,2)时截距最大,
过点A(0,2)时截距最大,
所以z的最小值为0-2×2=-4.
即 •
• 的最小值是-4.
的最小值是-4.
故答案为-4.
点评:本题考查了平面向量数量积的运算,考查了数学转化思想,训练了线性目标函数最值的求法,解答此类问题,最好的方法是把线性目标函数转化为直线方程的斜截式,把求目标函数的最值问题转化为求直线在y轴上的截距最大或最小问题.是中档题.
分析:由不等式组画出可行域,再由给出的两个点的坐标写出
 •
• 的表达式,利用线性规划知识求线性目标函数的最小值.
的表达式,利用线性规划知识求线性目标函数的最小值.解答:由不等式组
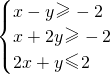 得可行域为△ABC的边界及其内部,如图,
得可行域为△ABC的边界及其内部,如图,
由x-y=-2,2x+y=2解得A(0,2).
由x-y=-2,x+2y=-2解得B(-2,0).
由x+2y=-2,2x+y=2解得C(2,-2).
∵M(x,y),N(1,-2),∴
 =(x,y),
=(x,y), =(1,-2).
=(1,-2).则
 •
• =x-2y.
=x-2y.令z=
 •
• =x-2y,则
=x-2y,则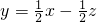 ,
,要使z最小,则直线
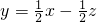 在y轴上的截距最大.
在y轴上的截距最大.由可行域可知,当直线
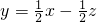 过点A(0,2)时截距最大,
过点A(0,2)时截距最大,所以z的最小值为0-2×2=-4.
即
 •
• 的最小值是-4.
的最小值是-4.故答案为-4.
点评:本题考查了平面向量数量积的运算,考查了数学转化思想,训练了线性目标函数最值的求法,解答此类问题,最好的方法是把线性目标函数转化为直线方程的斜截式,把求目标函数的最值问题转化为求直线在y轴上的截距最大或最小问题.是中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
已知x,y满足不等式组
则z=20-2y+x的最大值是( )
|
| A、21 | B、23 | C、25 | D、27 |