若椭圆的两个焦点与其中一个短轴端点恰好连成等腰直角三角形.则该椭圆的离心率为( )A．$\frac{1}{2}$B．$\frac{{\sqrt{2}}}{2}$C．$\frac{{\sqrt{3}}}{2}$D．$\frac{1}{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

2．若椭圆的两个焦点与其中一个短轴端点恰好连成等腰直角三角形，则该椭圆的离心率为（　　）

A．

$\frac{1}{2}$

B．

$\frac{{\sqrt{2}}}{2}$

C．

$\frac{{\sqrt{3}}}{2}$

D．

$\frac{1}{3}$

分析椭圆的两个焦点与其中一个短轴端点恰好连成等腰直角三角形，b=c，可得a=$\sqrt{2}$c，即可求出椭圆的离心率．

解答解：∵椭圆的两个焦点与其中一个短轴端点恰好连成等腰直角三角形，
∴b=c，
∴a=$\sqrt{2}$c，
∴e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$．
故选：B．

点评本题考查椭圆的离心率，考查学生的计算能力，确定b=c是关键．

练习册系列答案

相关题目

16．

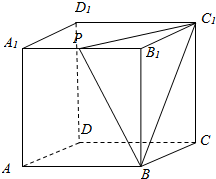如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，A₁B₁的中点是P，过点A₁作截面PBC₁平行的截面，则该截面的面积为（　　）

17．若直线y=3x-1是曲线y=ax³的一条切线，则a=4．

14．函数f（x）=log₂（x²-4x+5）的零点为2．

1．已知倾斜角为$\frac{2π}{3}$的直线l过抛物线y=$\frac{1}{4}$x²的焦点，则直线l被圆x²+y²+4y-5=0截得的弦长为3$\sqrt{3}$．

7．若关于x的函数y=（log${\;}_{\frac{1}{2}}$a）^x是R上的减函数，则实数a的取值范围是（$\frac{1}{2}$，1）．

14．已知向量$\overrightarrow a=（4，5cos（α+\;\frac{π}{6}）），\overrightarrow b=（3，-4tan（α+\frac{π}{6}）），\;α∈（0，\frac{π}{2}），\;\overrightarrow a⊥\overrightarrow b$，
（1）求|$\overrightarrow a-2\overrightarrow b|$；
（2）求$sin（2α+\frac{π}{12}）$的值．

11．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右顶点，上顶点分别为M、N，过其左焦点F作直线l垂直于x轴，且与椭圆在第二象限交于点P，$\overrightarrow{MN}$=λ$\overrightarrow{OP}$
（1）求证：a=$\sqrt{b}$；
（2）若椭圆的弦AB过点E（2，0）并与坐标轴不垂直，设点A关于x轴的对称点A，直线A₁B与x轴交于点R（5，0），求椭圆C的方程．

12．已知指数函数y=f（x）的图象过点（$\frac{1}{2}$，$\frac{\sqrt{2}}{2}$），则log₂f（2）的值为（　　）

试题分类