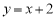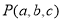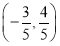题目内容
已知函数 是偶函数.
是偶函数.
(1)求 的值;
的值;
(2)设 ,若函数
,若函数 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围。
的取值范围。
(1)- ;(2){a
;(2){a a>1或a=-3}
a>1或a=-3}
【解析】
试题分析:(1)根据偶函数可知f(x)=f(-x),取x=-1代入即可求出k的值;
(2)函数f(x)与g(x)的图象有且只有一个公共点,则方程f(x)=g(x)有且只有一个实根,化简可得2x+ =a•2x?
=a•2x? a有且只有一个实根,令t=2x>0,则转化成方程(a?1)t2?
a有且只有一个实根,令t=2x>0,则转化成方程(a?1)t2? at?1=0有且只有一个正根,讨论a=1,以及△=0与一个正根和一个负根,三种情形,即可求出实数a的取值范围.
at?1=0有且只有一个正根,讨论a=1,以及△=0与一个正根和一个负根,三种情形,即可求出实数a的取值范围.
试题解析:(1)∵函数 f(x)= (
( +1)+kx(k∈R)是偶函数
+1)+kx(k∈R)是偶函数
∴ f(-x)= (
( +1)-kx=
+1)-kx= -kx=
-kx= (4x+1)-(k+1)x=
(4x+1)-(k+1)x= (4x+1)+kx恒成立
(4x+1)+kx恒成立
∴-(k+1)=k,则k=- 4分
4分
(2)g(x)= (a·
(a· -
- a),
a),
函数 f(x)与g(x)的图象有且只有一个公共点,即方程 f(x)=g(x)只有一个解
由已知得 (4x+1)-
(4x+1)- x=
x= (a·
(a· -
- a)
a)
∴
 =
= (a·
(a· -
- a),∴
a),∴ 且
且 =
= 8分
8分
设 。
。
设h(t)=(a-1)t2- at-1,若a-1>0,∵h(0)=-1<0,∴恰好有一正解,a>1满足题意。
at-1,若a-1>0,∵h(0)=-1<0,∴恰好有一正解,a>1满足题意。
若a-1=0,a=1,不满足题意。
若a-1<0,即a<1时, =0的a=-3或a=
=0的a=-3或a= ,
,
当a=-3时t= 满足题意。
满足题意。
当a= 时,t=-2(舍去) 11分
时,t=-2(舍去) 11分
综上:a的取值范围是{a a>1或a=-3} 12分
a>1或a=-3} 12分
考点:对数函数图像与性质的综合应用.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目