题目内容
设正数数列 为等比数列,
为等比数列, ,记
,记 .
.
(1)求 和
和 ;
;
(2)证明: 对任意的
 ,有
,有 成立.
成立.
(1) ,
,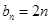 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)对照条件易得等比数列的通项公式 ,进而得
,进而得 ;(2)对于与自然数有关的命题的证明可优先考虑用数学归纳法,用数学归纳法证题时,首先要掌握好数学归纳法证题的规范、完整的证题步骤,而真正的难点和重点是由假设来推导第
;(2)对于与自然数有关的命题的证明可优先考虑用数学归纳法,用数学归纳法证题时,首先要掌握好数学归纳法证题的规范、完整的证题步骤,而真正的难点和重点是由假设来推导第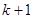 步,这里要充分地利用假设,若是对于恒等式的证明在利用了假设以后就很容易推导出第
步,这里要充分地利用假设,若是对于恒等式的证明在利用了假设以后就很容易推导出第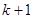 步,但是对于不等式的证明在利用了假设以后还不能一下子就推导出第
步,但是对于不等式的证明在利用了假设以后还不能一下子就推导出第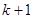 步,还需要对照目标进行适当的放缩处理才能推导出第
步,还需要对照目标进行适当的放缩处理才能推导出第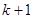 步,放缩处理是有难度,且需要技巧的,这需要在学习中去积累.
步,放缩处理是有难度,且需要技巧的,这需要在学习中去积累.
试题解析: (1)依题意可知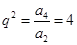 ,又
,又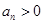 ,所以
,所以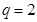 ,从而
,从而 ,进而有
,进而有 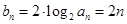 . 4分
. 4分
(2)证明:①当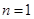 时,左边
时,左边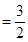 ,右边
,右边 ,因为
,因为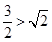 ,所以不等式成立. 5分
,所以不等式成立. 5分
②假设当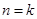 时,不等式成立,即
时,不等式成立,即 成立. 7分
成立. 7分
那么当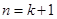 时,则左边
时,则左边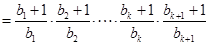


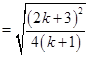
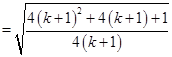
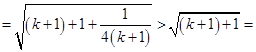 右边 12分
右边 12分
所以当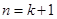 时,不等式也成立.
时,不等式也成立.
由①、②可得对任意的
 ,都有
,都有 恒成立. 14分
恒成立. 14分
(另解:此题也可直接用放缩法证明.即用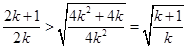 )
)
考点:1.等比数列知识;2.数学归纳法在证明不等式方面的应用;3.放缩法证明不等式.

练习册系列答案
相关题目
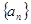 中,
中,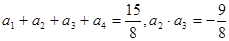 ,则
,则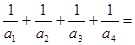
 中,
中, ,
, ,求
,求 和
和 .
.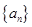 满足:
满足: ,其中
,其中 .
. 是等比数列;
是等比数列; ,求数列
,求数列 的最大项.
的最大项. 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 N,都有
N,都有
 为常数,且
为常数,且 .
. 与
与 函数关系为
函数关系为 ,数列
,数列 满足
满足 ,点
,点 落在
落在  ,
, 的通项公式;
的通项公式; 的前
的前 ,使
,使 恒成立时,求
恒成立时,求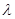 的最小值.[
的最小值.[ (n∈N*).
(n∈N*). +
+ }是等比数列,并求数列{an}的通项an
}是等比数列,并求数列{an}的通项an an,数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
an,数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围. 首项为
首项为 ,公比为q,求(1)该数列的前n项和
,公比为q,求(1)该数列的前n项和 。
。 不是等比数列
不是等比数列 数列
数列 满足:
满足:
 .
. 是等比数列(要指出首项与公比);
是等比数列(要指出首项与公比); 的通项公式.
的通项公式. 满足:
满足: ,则
,则 ;
;