题目内容
(本小题满分12分)设函数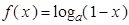 ,
,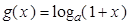 (
(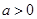 且
且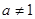 )。
)。
(1)设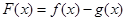 ,判断
,判断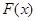 的奇偶性并证明;
的奇偶性并证明;
(2)若关于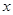 的方程
的方程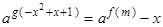 有两个不等实根,求实数
有两个不等实根,求实数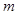 的范围;
的范围;
(3)若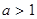 且在
且在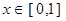 时,
时,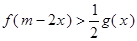 恒成立,求实数
恒成立,求实数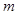 的范围。
的范围。
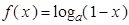 ,
,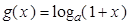 (
(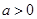 且
且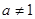 )。
)。(1)设
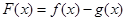 ,判断
,判断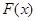 的奇偶性并证明;
的奇偶性并证明;(2)若关于
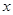 的方程
的方程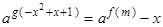 有两个不等实根,求实数
有两个不等实根,求实数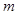 的范围;
的范围;(3)若
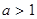 且在
且在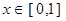 时,
时,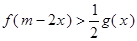 恒成立,求实数
恒成立,求实数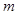 的范围。
的范围。(1)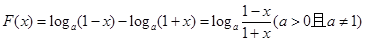
其中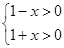 ∴
∴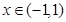
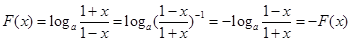
∴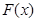 为奇函数。 (2)
为奇函数。 (2)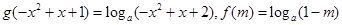
原方程有两个不等实根即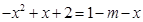 有两个不等实根。… 其中
有两个不等实根。… 其中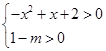 ∴
∴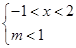 即
即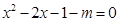 在
在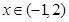 上有两个不等实根。…
上有两个不等实根。…
记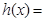
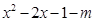 ,对称轴x=1,由
,对称轴x=1,由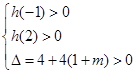 解得
解得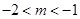
(3)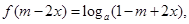
即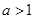 且
且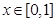 时
时 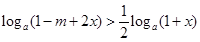 恒成立
恒成立
∴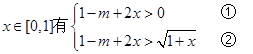 恒成立,
恒成立,
由①得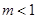
令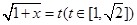 ∴由②得
∴由②得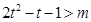 在
在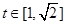 时恒成立
时恒成立
记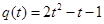 即
即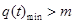 ,
,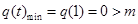
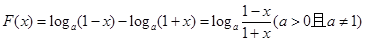
其中
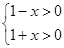 ∴
∴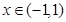
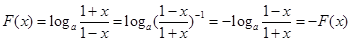
∴
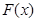 为奇函数。 (2)
为奇函数。 (2)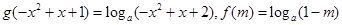
原方程有两个不等实根即
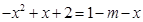 有两个不等实根。… 其中
有两个不等实根。… 其中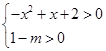 ∴
∴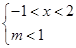 即
即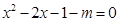 在
在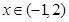 上有两个不等实根。…
上有两个不等实根。…记
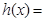
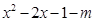 ,对称轴x=1,由
,对称轴x=1,由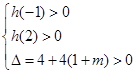 解得
解得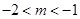
(3)
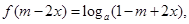
即
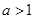 且
且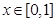 时
时 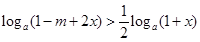 恒成立
恒成立∴
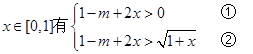 恒成立,
恒成立,由①得
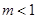
令
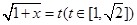 ∴由②得
∴由②得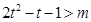 在
在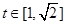 时恒成立
时恒成立记
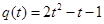 即
即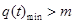 ,
,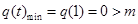
略

练习册系列答案
相关题目
 ,
, ,其中
,其中 R.
R. 的单调性;
的单调性;
 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数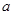 的取值范围;
的取值范围;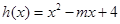 ,当
,当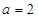 时,若
时,若 ,
, ,总有
,总有 成立,求实数
成立,求实数 的取值范围。
的取值范围。 ,
, ,记
,记 .
. ,且
,且 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;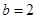 ,且
,且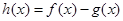 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围; ,设函数
,设函数 的图象
的图象 与函数
与函数 图象
图象 交于点
交于点 、
、 ,过线段
,过线段 的中点作
的中点作 轴的垂线分别交
轴的垂线分别交 、
、 ,请判断
,请判断 切线能否平行,并说明你的理由.
切线能否平行,并说明你的理由. 米 ,房屋正面的造价为400元/平方米,房屋侧面的造价为150元/平方米,屋顶和地面的造价费用合计为5800元,如果墙高为3米,且不计房屋背面的费用.(1)把房屋总造价y表示成x的函数,并写出该函数的定义域;(2)当侧面的长度为多少时,总造价最低?最低造价是多少?
米 ,房屋正面的造价为400元/平方米,房屋侧面的造价为150元/平方米,屋顶和地面的造价费用合计为5800元,如果墙高为3米,且不计房屋背面的费用.(1)把房屋总造价y表示成x的函数,并写出该函数的定义域;(2)当侧面的长度为多少时,总造价最低?最低造价是多少? ,方程
,方程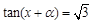 的一个解为
的一个解为 ,则
,则 等于 .
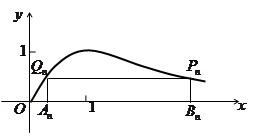
等于 .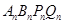 的一边
的一边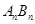 在
在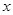 轴上,另两个顶点
轴上,另两个顶点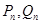 在函数
在函数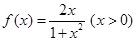 的图像上(其中点
的图像上(其中点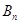 的坐标为
的坐标为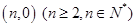 ),矩形
),矩形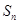 ,则
,则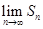 =" "
=" " 
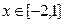 时,函数
时,函数 的值域是___________
的值域是___________ 的定义域是
的定义域是