题目内容
若抛物线y=
在点(a,a2)处的切线与两坐标轴围成的三角形的面积为16,则a=( )
| x | 2 |
分析:确定点(a,a2)处的切线方程,进而可求切线与两坐标轴围成的三角形的面积,即可求得a的值.
解答:解:求导数可得y′=2x,所以在点(a,a2)处的切线方程为:y-a2=2a(x-a),
令x=0,得y=-a2;令y=0,得x=
a.
所以切线与两坐标轴围成的三角形的面积S=
×|-a2|×|
a|=
|a3|=16,解得a=±4.
故选B.
令x=0,得y=-a2;令y=0,得x=
| 1 |
| 2 |
所以切线与两坐标轴围成的三角形的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
故选B.
点评:本题考查导数的几何意义,考查三角形面积的计算,确定切线方程是关键.

练习册系列答案
相关题目
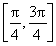
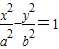 的一条渐近线垂直,则双曲线的离心率等于 .
的一条渐近线垂直,则双曲线的离心率等于 .