题目内容
若抛物线y=x2在点(1,1)处的切线与双曲线
-
=1的一条渐近线垂直,则双曲线的离心率等于
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
分析:先利用导数求出切线的斜率,得到切线方程,再根据互相垂直的直线的性质求出渐近线的斜率,最后根据离心率公式求出所求即可.
解答:解:∵y=x2∴y′=2x则y′|x=1=2
∴抛物线y=x2在点(1,1)处的切线方程为y=2x-1
∵切线与双曲线
-
=1的一条渐近线垂直,
∴双曲线
-
=1的一条渐近线的斜率为-
则-
=-
不妨设a=2,b=1则c=
∴e=
=
故答案为:
∴抛物线y=x2在点(1,1)处的切线方程为y=2x-1
∵切线与双曲线
| x2 |
| a2 |
| y2 |
| b2 |
∴双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
不妨设a=2,b=1则c=
| 5 |
∴e=
| c |
| a |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及双曲线的简单性质,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
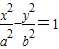 的一条渐近线垂直,则双曲线的离心率等于 .
的一条渐近线垂直,则双曲线的离心率等于 .