题目内容
已知R上的不间断函数g(x)满足:①当x>0时,g'(x)>0恒成立;②对任意的x∈R都有g(x)=g(-x).又函数f(x)满足:对任意的x∈R,都有f(
+x)=-f(x)成立,当x∈[0,
]时,f(x)=x3-3x.若关于x的不等式g[f(x)]≤g(a2-a+2)对x∈[-3,3]恒成立,则a的取值范围
| 3 |
| 3 |
a≥1或a≤0.
a≥1或a≤0.
.分析:由函数g(x)满足:①当x>0时,g'(x)>0恒成立;②对任意x∈R都有g(x)=g(-x),说明函数g(x)为R上的偶函数且在[0,+∞)上为单调递增函数,且有g|(x|)=g(x),所以g[f(x)]≤g(a2-a+2)?|f(x)|≤|a2-a+2|对x∈[-3,3]恒成立,只要使得|f(x)|max≤|a2-a+2|min,然后解此不等式即可.
解答:解:因为函数g(x)满足:当x>0时,g'(x)>0恒成立,且对任意x∈R都有g(x)=g(-x),
∴函数g(x)为R上的偶函数且在[0,+∞)上为单调递增函数,且有g|(x|)=g(x),
∴g[f(x)]≤g(a2-a+2)在R上恒成立,
∴|f(x)|≤|a2-a+2|对x∈[-
-2
,
-2
]恒成立,
只要使得定义域内|f(x)|max≤|a2-a+2|min,
由于当x∈[-3,3]时,f(x)=x3-3x,
求导得:f′(x)=3x2-3=3(x+1)(x-1),
该函数过点(-3,0),(0,0),( 3,0),且函数在x=-1处取得极大值f(-1)=2,在x=1处取得极小值f(1)=-2,
又由于对任意的x∈R都有f(
+x)=-f(x),
∴f(2
+x)=-f(
+x)=f(x)成立,则函数f(x)为周期函数且周期为T=2
,
所以函数f(x)在x∈[-
-2
,
-2
]的最大值为2,所以令2≤|a2-a+2|
解得:a≥1或a≤0.
故答案为:a≥1或a≤0.
∴函数g(x)为R上的偶函数且在[0,+∞)上为单调递增函数,且有g|(x|)=g(x),
∴g[f(x)]≤g(a2-a+2)在R上恒成立,
∴|f(x)|≤|a2-a+2|对x∈[-
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
只要使得定义域内|f(x)|max≤|a2-a+2|min,
由于当x∈[-3,3]时,f(x)=x3-3x,
求导得:f′(x)=3x2-3=3(x+1)(x-1),
该函数过点(-3,0),(0,0),( 3,0),且函数在x=-1处取得极大值f(-1)=2,在x=1处取得极小值f(1)=-2,
又由于对任意的x∈R都有f(
| 3 |
∴f(2
| 3 |
| 3 |
| 3 |
所以函数f(x)在x∈[-
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
解得:a≥1或a≤0.
故答案为:a≥1或a≤0.
点评:此题考查了利用导函数求得函数在定义域上为单调递增函数,还考查了函数的周期的定义,及利用周期可以求得当x∈[-
,
]时,f(x)=x3-3x,的值域为[-2,2],还考查了函数恒成立.
| 3 |
| 3 |

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
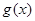 满足:①当
满足:①当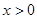 时,
时,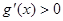 恒成立;②对任意的
恒成立;②对任意的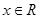 都有
都有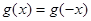 。又函数
。又函数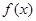 满足:对任意的
满足:对任意的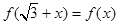 成立,当
成立,当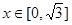 时,
时,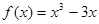 。若关于
。若关于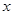 的不等式
的不等式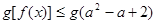 对
对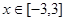 恒成立,则
恒成立,则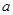 的取值范围( )
的取值范围( )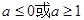 B.
B.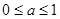 C.
C.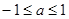 D.
D.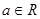
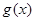 满足:①当
满足:①当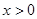 时,
时,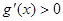 恒成立;②对任意的
恒成立;②对任意的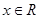 都有
都有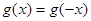 。又函数
。又函数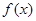 满足:对任意的
满足:对任意的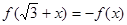 成立,当
成立,当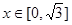 时,
时,
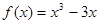 。若关于
。若关于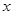 的不等式
的不等式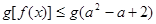 对
对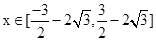 恒成立,则
恒成立,则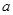 的取值范围( )
的取值范围( )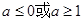 B.
B. 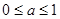 C.
C.
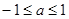 D.
D.